Implicit Differentiation
The techniques we learned allow us to differentiate the functions like $$${y}={\sqrt[{{3}}]{{{{x}}^{{2}}+{\sin{{\left({x}\right)}}}}}}$$$ or $$${y}=\frac{{\tan{{\left({x}\right)}}}}{{{{e}}^{{{\sin{{\left({x}\right)}}}}}}}$$$, or, in general, $$${y}={f{{\left({x}\right)}}}$$$. But what to do if we can't express $$${y}$$$ in terms of $$${x}$$$ or if the expression would be very complex?
Consider $$${{x}}^{{2}}+{{y}}^{{2}}={16}$$$. This is the equation of a circle, and we can solve it for $$${y}$$$: $$${y}=\pm\sqrt{{{16}-{{x}}^{{2}}}}$$$. But here we obtained two functions and we have more work than earlier.
For example, $$${{x}}^{{3}}+{{y}}^{{3}}={2}{x}{y}$$$ can be solved for $$${y}$$$, but the expression would be very complex, and, finally, $$${{x}}^{{2}}+{{y}}^{{4}}={\sin{{\left({x}+{y}\right)}}}$$$ can't be solved explicitly for $$${x}$$$.
What to do in such cases?
Fortunately, we don't need to express $$${y}$$$ in terms of $$${x}$$$. We can use implicit differentiation. This consists in differentiating both sides of the equation with respect to $$${x}$$$ and then solving the resulting equation for $$${y}'$$$. We assume that the given equation determines $$${y}$$$ implicitly as a differentiable function of $$${x}$$$, so that the method of implicit differentiation could be applied.
Example 1. Find the equation of the tangent line to $$${{x}}^{{2}}+{{y}}^{{2}}={25}$$$ at the point $$$(3,4)$$$.
To find the slope of the tangent line, we need the derivative of the function. Here, the function is given implicitly; so, we use implicit differentiation.
Differentiate both sides of the equation with respect to $$${x}$$$ and remember that $$${y}$$$ is a function of $$${x}$$$.
$$$\frac{{d}}{{{d}{x}}}{\left({{x}}^{{2}}+{{y}}^{{2}}\right)}=\frac{{d}}{{{d}{x}}}{\left({25}\right)}$$$
$$$\frac{{d}}{{{d}{x}}}{\left({{x}}^{{2}}\right)}+\frac{{d}}{{{d}{x}}}{\left({{y}}^{{2}}\right)}={0}$$$
$$${2}{x}+{2}{y}\frac{{{d}{y}}}{{{d}{x}}}={0}$$$.
Notice how we used the chain rule while differentiating $$${{y}}^{{2}}$$$ : $$$\frac{{d}}{{{d}{x}}}{\left({{y}}^{{2}}\right)}=\frac{{d}}{{{d}{y}}}{\left({{y}}^{{2}}\right)}\cdot\frac{{{d}{y}}}{{{d}{x}}}={2}{y}\frac{{{d}{y}}}{{{d}{x}}}$$$.
Solving for $$$\frac{{{d}{y}}}{{{d}{x}}}$$$ gives $$$\frac{{{d}{y}}}{{{d}{x}}}=-\frac{{x}}{{y}}$$$.
Therefore, at the point $$$(3,4)$$$, the slope of the tangent line is $$$-\frac{{3}}{{4}}$$$, and the equation of the tangent line is $$${y}-{4}=-\frac{{3}}{{4}}{\left({x}-{3}\right)}$$$, or $$${y}=-\frac{{3}}{{4}}{x}+\frac{{25}}{{4}}$$$.
As can be seen, implicit differentiation can make differentiation easier and can save loads of time.
Example 2. Where is the tangent line horizontal or vertical to $$${{x}}^{{3}}+{{y}}^{{3}}={3}{x}{y}$$$ (folium of Descartes)?
Differentiating both sides of the equation with respect to $$${x}$$$, we obtain $$$\frac{{d}}{{{d}{x}}}{\left({{x}}^{{3}}+{{y}}^{{3}}\right)}=\frac{{d}}{{{d}{x}}}{\left({3}{x}{y}\right)}$$$, or $$$\frac{{d}}{{{d}{x}}}{\left({{x}}^{{3}}\right)}+\frac{{d}}{{{d}{x}}}{\left({{y}}^{{3}}\right)}={3}\frac{{d}}{{{d}{x}}}{\left({x}{y}\right)}$$$.
To differentiate $$${x}{y}$$$, we need to use the product rule: $$$\frac{{d}}{{{d}{x}}}{\left({x}{y}\right)}=\frac{{d}}{{{d}{x}}}{\left({x}\right)}{y}+{x}\frac{{d}}{{{d}{x}}}{\left({y}\right)}={y}+{x}\frac{{{d}{y}}}{{{d}{x}}}$$$.
To differentiate $$${{y}}^{{3}}$$$, we need to use the chain rule: $$$\frac{{d}}{{{d}{x}}}{{y}}^{{3}}=\frac{{d}}{{{d}{y}}}{\left({{y}}^{{3}}\right)}\cdot\frac{{{d}{y}}}{{{d}{x}}}={3}{{y}}^{{2}}\frac{{{d}{y}}}{{{d}{x}}}$$$.
So, the equation can be rewritten as
$$${3}{{x}}^{{2}}+{3}{{y}}^{{2}}\frac{{{d}{y}}}{{{d}{x}}}={3}{\left({y}+{x}\frac{{{d}{y}}}{{{d}{x}}}\right)}$$$.
Solving for $$$\frac{{{d}{y}}}{{{d}{x}}}$$$ gives $$$\frac{{{d}{y}}}{{{d}{x}}}=\frac{{{y}-{{x}}^{{2}}}}{{{{y}}^{{2}}-{x}}}$$$.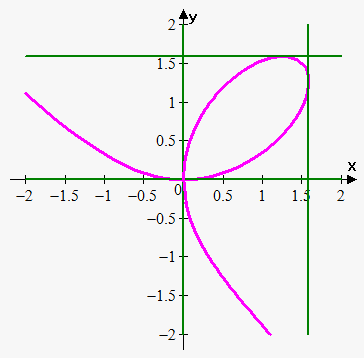
The tangent line is horizontal when $$$\frac{{{d}{y}}}{{{d}{x}}}={0}$$$, or $$${y}-{{x}}^{{2}}={0}$$$, which gives $$${y}={{x}}^{{2}}$$$.
If we now substitute $$${y}$$$ in the initial equation with the obtained expression, we have that $$${{x}}^{{3}}+{{\left({{x}}^{{2}}\right)}}^{{3}}={3}{x}\cdot{{x}}^{{2}}$$$, or $$${{x}}^{{6}}-{2}{{x}}^{{3}}={0}$$$.
Thus, the tangent line is horizontal when either $$${x}={0}$$$ or $$${x}={{2}}^{{\frac{{1}}{{3}}}}$$$.
So, the tangent line is horizontal at the points $$$(0,0)$$$ and $$${\left({{2}}^{{\frac{{1}}{{3}}}},{{\left({{2}}^{{\frac{{1}}{{3}}}}\right)}}^{{2}}\right)}={\left({{2}}^{{\frac{{1}}{{3}}}},{{2}}^{{\frac{{2}}{{3}}}}\right)}\approx{\left({1.26},{1.59}\right)}$$$.
The tangent line is vertical when the denominator in the expression for $$$\frac{{{d}{y}}}{{{d}{x}}}$$$ is $$$0$$$, or $$${{y}}^{{2}}={x}.$$$ Another method is to observe that the equation of the curve is unchanged when $$${x}$$$ and $$${y}$$$ are interchanged, so the curve is symmetric about the line $$${y}={x}$$$. This means that the horizontal tangents at $$$(0, 0)$$$ and $$${\left({{2}}^{{\frac{{1}}{{3}}}},{{2}}^{{\frac{{2}}{{3}}}}\right)}$$$ correspond to the vertical tangents at $$$(0, 0)$$$ and $$${\left({{2}}^{{\frac{{2}}{{3}}}},{{2}}^{{\frac{{1}}{{3}}}}\right)}$$$.
Example 3. Find $$${y}'=\frac{{{d}{y}}}{{{d}{x}}}$$$, where $$${\sin{{\left({x}+{y}\right)}}}={{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}$$$.
We use the chain rule and the product rule.
$$$\frac{{d}}{{{d}{x}}}{\left({\sin{{\left({x}+{y}\right)}}}\right)}=\frac{{d}}{{{d}{x}}}{\left({{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}\right)}$$$
$$${\cos{{\left({x}+{y}\right)}}}\cdot\frac{{d}}{{{d}{x}}}{\left({x}+{y}\right)}={{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}\cdot\frac{{d}}{{{d}{x}}}{\left({{x}}^{{2}}{{y}}^{{2}}\right)}$$$
$$${\cos{{\left({x}+{y}\right)}}}{\left({1}+{y}'\right)}={{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}{\left(\frac{{d}}{{{d}{x}}}{\left({{x}}^{{2}}\right)}{{y}}^{{2}}+{{x}}^{{2}}\frac{{d}}{{{d}{x}}}{\left({{y}}^{{2}}\right)}\right)}$$$
$$${\cos{{\left({x}+{y}\right)}}}{\left({1}+{y}'\right)}={{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}{\left({2}{x}{{y}}^{{2}}+{2}{y}{{x}}^{{2}}{y}'\right)}$$$
$$${\cos{{\left({x}+{y}\right)}}}+{\cos{{\left({x}+{y}\right)}}}{y}'={2}{x}{{y}}^{{2}}{{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}+{2}{y}{{x}}^{{2}}{{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}{y}'$$$.
Solving for $$${y}'$$$ gives $$${y}'=\frac{{{\cos{{\left({x}+{y}\right)}}}-{2}{x}{{y}}^{{2}}{{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}}}{{{2}{y}{{x}}^{{2}}{{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}-{\cos{{\left({x}+{y}\right)}}}}}$$$.
Since, from the equation of a curve, $$${\sin{{\left({x}+{y}\right)}}}={{e}}^{{{{x}}^{{2}}{{y}}^{{2}}}}$$$, we can write equivalently $$${y}'=\frac{{{\cos{{\left({x}+{y}\right)}}}-{2}{x}{{y}}^{{2}}{\sin{{\left({x}+{y}\right)}}}}}{{{2}{y}{{x}}^{{2}}{\sin{{\left({x}+{y}\right)}}}-{\cos{{\left({x}+{y}\right)}}}}}$$$.
