Graphing Calculator
Graph functions, points, inequalities
A free online 2D graphing calculator (plotter), or curve calculator, that can plot piecewise, linear, quadratic, cubic, quartic, polynomial, trigonometric, hyperbolic, exponential, logarithmic, inverse functions given in different forms: explicit, implicit, polar, and parametric. It can also graph conic sections, arbitrary inequalities or systems of inequalities, slope fields (vector fields or direction fields), and visualize the Riemann sum. The plots can be styled and customized according to needs.
To draw a parabola, circle, ellipse or hyperbola, choose the "Implicit" option.
You can pass a function as a parameter: https://www.emathhelp.net/calculators/calculus-1/online-graphing-calculator/?y=sin(x)&y=cos(x) will draw y=sin(x) and y=cos(x).
Related calculator: 3D Graphing Calculator
Pan the graph (move it) by holding the Shift key and dragging the graph with the mouse.
Zoom the graph in and out by holding the Shift key and using the mouse wheel.
The above operations can be very slow for more than 2 graphs. To avoid it, delete all graphs, pan and zoom, and then plot the graphs again.
The Online Graphing Calculator is a digital tool for visualizing different types of curves. It allows you to plot explicit, implicit, parametric, and polar curves, as well as display a set of points or a system of inequalities.
How to Use the Graphing Calculator?
Input
Begin by entering the function(s) you want to visualize into the provided input field(s). Use the available options to customize your graph(s) as needed. This includes adjusting the axes, adding labels, and selecting various graph styles to suit your preferences.
Calculation
Click the "Add" button, and the calculator will quickly generate a graph based on your input.
Result
Examine the generated graph to gain valuable insight into the behavior of your function. Identify key points, intersection points, and so on.
What Is Graphing?
Graphing, in mathematics and data visualization, refers to creating visual representations of data or functions on a coordinate plane. These visual representations are called graphs or plots. Graphs are essential tools for understanding and analyzing relationships between variables, patterns in data, and the behavior of functions.
What Is Meant by Graphing Functions?
Function graphing is a fundamental concept that visualizes the relationships between variables. These relationships can be represented by equations that determine how one variable (output or dependent) depends on another variable (input or independent).
A function is typically represented using a formula or rule. It is denoted as $$$f(x)$$$, where $$$f$$$ is the function's name, and $$$x$$$ is the input variable. The function takes an input value $$$x$$$, processes it using the formula, and produces an output value $$$f(x)$$$.
For example, consider the following function:
$$f(x)=2x+3$$In this function, $$$x$$$ is the input variable, and the formula $$$2x+3$$$ describes how the output depends on the input. If you plug in a specific value for $$$x$$$, you can calculate the corresponding value of $$$f(x)$$$. For example, if $$$x=5$$$, then $$$f(5)=2\cdot5+3=13$$$.
Graphical Representation
To understand the behavior of a function, we often create a graphical representation of it on a coordinate plane. The x-axis represents the input variable, and the y-axis represents the output variable. Each point on the graph corresponds to a pair of input and output values.
Let's graph the function $$$f(x)=2x+3$$$. To do this, we can choose several values of $$$x$$$, calculate the corresponding $$$f(x)$$$ values, plot these points on the graph, and then graph a line through these points, since $$$f(x)=2x+3$$$ represents a line.
Here's the table of values:
| $$$x$$$ | $$$f(x)$$$ |
| $$$-2$$$ | $$$2\cdot(-2)+3=-1$$$ |
| $$$-1$$$ | $$$2\cdot(-1)+3=1$$$ |
| $$$0$$$ | $$$2\cdot0+3=3$$$ |
| $$$1$$$ | $$$2\cdot1+3=5$$$ |
The resulting graph is shown below:
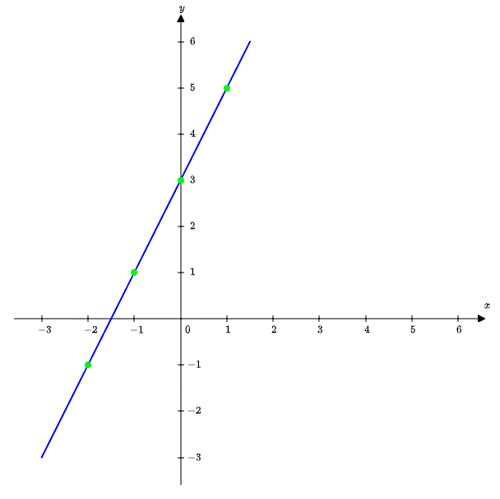
As you move along the x-axis, the y-values change according to the formula.
Concepts:
- Domain and Range: The domain of a function is the set of all possible input values, and the range is the set of all actual output values. In our example, the domain is all real numbers, and the range is all real numbers.
- Types of Functions: Functions can be of different types: linear, quadratic, exponential, logarithmic, trigonometric, and more. Each type has its unique characteristics and graphical representation.
- Slope and Rate of Change: The slope of a function's graph represents the rate at which the output changes relative to the input. Steeper slopes indicate faster changes, while shallower slopes represent slower changes.
Why Choose Our Graphing Calculator?
Versatility
The tool can plot explicit, implicit, polar, and parametric curves. In addition, it can graph tangent and normal lines, systems of inequalities, slope fields, sets of points, etc. There are many options to customize our graphs.
User-Friendly Interface
Our calculator has been carefully designed for ease of use. You'll find value in its user-friendly interface, which simplifies the graphing process.
Accuracy
Our calculator is carefully designed to provide consistently accurate results every time you use it.
FAQ
What is the meaning of graphing?
Graphing is the process of visually representing data or functions on a coordinate plane. It involves plotting points, lines, or curves to illustrate relationships between variables, making complex information more accessible and understandable.
How do you do the graphing method?
To graph, enter a mathematical function or data into the calculator and it will generate a graphical representation. For data, the calculator will plot points on a coordinate plane, and for a function, it will create a graph showing how the output depends on the input.
What types of graphs can I create with the calculator?
Our calculator supports a wide range of functions you can graph: explicit, implicit, polar, and parametric functions. You can also plot a set of points and much, much more. This allows you to create graphs to visualize data trends, explore functions, and analyze relationships between variables.
Why is graphing so important in science?
Graphing is important in science because it allows scientists to visualize and analyze data effectively. This helps identify trends, correlations, and patterns in experimental results. Graphs also help scientists communicate their findings, make predictions, and understand relationships between variables, which is critical for scientific research and experimentation.
