Area Enclosed by Parametric Curves
We know that area under the curve $$${y}={F}{\left({x}\right)}$$$ is $$${A}={\int_{{a}}^{{b}}}{F}{\left({x}\right)}{d}{x}$$$ where $$${f{{\left({x}\right)}}}\ge{0}$$$.
If curve is given by parametric equations $$${x}={f{{\left({t}\right)}}}$$$ and $$${y}={g{{\left({t}\right)}}}$$$ then using substitution rule with $$${x}={f{{\left({t}\right)}}}$$$ we have that $$${d}{x}={f{'}}{\left({t}\right)}{d}{t}$$$ and since $$${x}$$$ is changing from $$${a}$$$ to $$${b}$$$ then $$${t}$$$ is changing from $$$\alpha={{f}}^{{-{1}}}{\left({a}\right)}$$$ to $$$\beta={{f}}^{{-{1}}}{\left({b}\right)}$$$. It is not always a case, sometimes $$${t}$$$ is changing from $$$\beta$$$ to $$$\alpha$$$.
So, $$${A}={\int_{{a}}^{{b}}}{F}{\left({x}\right)}{d}{x}={\int_{\alpha}^{\beta}}{F}{\left({f{{\left({t}\right)}}}\right)}{f{'}}{\left({t}\right)}{d}{t}={\int_{\alpha}^{\beta}}{g{{\left({t}\right)}}}{f{'}}{\left({t}\right)}{d}{t}$$$.
Area Enclosed by Parametric Curves: $$${A}={\int_{{\alpha}}^{{\beta}}}{g{{\left({t}\right)}}}{f{'}}{\left({t}\right)}{d}{t}$$$ (or $$${\int_{\beta}^{\alpha}}{g{{\left({t}\right)}}}{f{'}}{\left({t}\right)}{d}{t}$$$).
Example. Find the area under one arch of cycloid. $$${x}={r}{\left({t}-{\sin{{\left({t}\right)}}}\right)}$$$, $$${y}={r}{\left({1}-{\cos{{\left({t}\right)}}}\right)}$$$.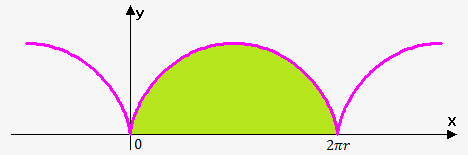
One arch of the cycloid is given by $$${0}\le{t}\le{2}\pi$$$.
We have that $$${x}_{{t}}'={r}{\left({1}-{\cos{{\left({t}\right)}}}\right)}$$$.
Therefore, $$${A}={\int_{{0}}^{{{2}\pi}}}{r}{\left({1}-{\cos{{\left({t}\right)}}}\right)}{r}{\left({1}-{\cos{{\left({t}\right)}}}\right)}{d}{t}=$$$
$$$={{r}}^{{2}}{\int_{{0}}^{{{2}\pi}}}{{\left({1}-{\cos{{\left({t}\right)}}}\right)}}^{{2}}{d}{t}={{r}}^{{2}}{\int_{{0}}^{{{2}\pi}}}{\left({1}-{2}{\cos{{\left({t}\right)}}}+{{\cos}}^{{2}}{\left({t}\right)}\right)}{d}{t}$$$.
Now, we need to use double angle formula and integral becomes:
$$${A}{{r}}^{{2}}{\int_{{0}}^{{{2}\pi}}}{\left({1}-{2}{\cos{{\left({t}\right)}}}+\frac{{1}}{{2}}{\left({1}+{\cos{{\left({2}{t}\right)}}}\right)}\right)}{d}{t}={{r}}^{{2}}{\int_{{0}}^{{{2}\pi}}}{\left(\frac{{3}}{{2}}-{2}{\cos{{\left({t}\right)}}}+\frac{{1}}{{2}}{\cos{{\left({2}{t}\right)}}}\right)}{d}{t}=$$$
$$$={{r}}^{{2}}{\left(\frac{{3}}{{2}}{t}-{2}{\sin{{\left({t}\right)}}}+\frac{{1}}{{4}}{\sin{{\left({2}{t}\right)}}}\right)}{{\mid}_{{0}}^{{{2}\pi}}}=$$$
$$$={{r}}^{{2}}{\left({\left(\frac{{3}}{{2}}{2}\pi-{2}{\sin{{\left({2}\pi\right)}}}+\frac{{1}}{{4}}{\sin{{\left({2}\cdot{2}\pi\right)}}}\right)}-{\left(\frac{{3}}{{2}}\cdot{0}-{2}{\sin{{\left({0}\right)}}}+\frac{{1}}{{4}}{\sin{{\left({2}\cdot{0}\right)}}}\right)}\right)}=$$$
$$$={{r}}^{{2}}{\left({\left({3}\pi-{2}\cdot{0}+\frac{{1}}{{4}}\cdot{0}\right)}-{\left({0}-{2}\cdot{0}+\frac{{1}}{{4}}\cdot{0}\right)}\right)}={3}\pi{{r}}^{{2}}$$$.
