Condition of Constancy of the Function

Fact. Suppose function $$${y}={f{{\left({x}\right)}}}$$$ is defined and continuous on interval $$${X}$$$ and has finite derivative $$${f{'}}{\left({x}\right)}$$$. Function $$${y}={f{{\left({x}\right)}}}$$$ is constant if and only if $$${f{'}}{\left({x}\right)}$$$ for all $$${x}$$$ in $$${X}$$$.

This fact means that if on some interval derivative of function equals 0 then function is constant their, its graph is just horizontal line.

Corollary. Suppose two function $$${y}={f{{\left({x}\right)}}}$$$ and $$${y}={g{{\left({x}\right)}}}$$$ are defined and continuous on interval $$${X}$$$, and have finite derivatives $$${f{'}}{\left({x}\right)}$$$ and $$${g{{\left({x}\right)}}}$$$. Function $$${y}={f{{\left({x}\right)}}}$$$ is constant if and only if $$${f{'}}{\left({x}\right)}$$$ for all $$${x}$$$ in $$${X}$$$. If $$${f{'}}{\left({x}\right)}={g{'}}{\left({x}\right)}$$$ on interval $$${X}$$$ then $$${f{{\left({x}\right)}}}={g{{\left({x}\right)}}}+{C}$$$, where $$${C}$$$ is a constant for all $$${x}$$$ in $$${X}$$$.

This corollary means that if functions have same derivatives on interval $$${X}$$$ then their difference is constant.

Example 1. Consider functions $$${f{{\left({x}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}$$$ and $$${g{{\left({x}\right)}}}={\operatorname{arcsin}{{\left(\frac{{x}}{{\sqrt{{{1}+{{x}}^{{2}}}}}}\right)}}}$$$.

They are defined and continuous on interval $$${\left(-\infty,\infty\right)}$$$.

Since $$${f{'}}{\left({x}\right)}=\frac{{1}}{{{1}+{{x}}^{{2}}}}$$$ and $$${g{'}}{\left({x}\right)}=\frac{{1}}{{{1}-{{\left(\frac{{x}}{\sqrt{{{1}+{{x}}^{{2}}}}}\right)}}^{{2}}}}\cdot\frac{{\sqrt{{{1}+{{x}}^{{2}}}}-\frac{{{{x}}^{{2}}}}{{\sqrt{{{1}+{{x}}^{{2}}}}}}}}{{{1}+{{x}}^{{2}}}}=\frac{{1}}{{{1}+{{x}}^{{2}}}}$$$ then according to corollary $$${\operatorname{arctan}{{\left({x}\right)}}}={\operatorname{arcsin}{{\left(\frac{{x}}{{\sqrt{{{1}+{{x}}^{{2}}}}}}\right)}}}+{C}$$$ on $$${\left(-\infty,\infty\right)}$$$.

To find constant plug any value of $$${x}$$$, for example, $$${x}={0}$$$: $$${\operatorname{arctan}{{\left({0}\right)}}}={\operatorname{arcsin}{{\left(\frac{{0}}{\sqrt{{{1}+{{0}}^{{2}}}}}\right)}}}+{C}$$$ or $$${C}={0}$$$.

So, we have the following fact: $$${\operatorname{arctan}{{\left({x}\right)}}}={\operatorname{arcsin}{{\left(\frac{{x}}{\sqrt{{{1}+{{x}}^{{2}}}}}\right)}}}$$$ for all $$${x}$$$.

Example 2. Consider functions $$${f{{\left({x}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}$$$ and $$${g{{\left({x}\right)}}}=\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}{x}}}{{{1}-{{x}}^{{2}}}}\right)}}}$$$.

It can be easily proven that $$${f{'}}{\left({x}\right)}={g{'}}{\left({x}\right)}$$$. However, function $$${g{{\left({x}\right)}}}$$$ is not defined when $$${x}=\pm{1}.$$$ So, $$$\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}{x}}}{{{1}-{{x}}^{{2}}}}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}+{C}$$$ on $$${\left(-\infty,-{1}\right)},{\left(-{1},{1}\right)},{\left({1},\infty\right)}$$$.

It is interesting that constant will be different for different intervals.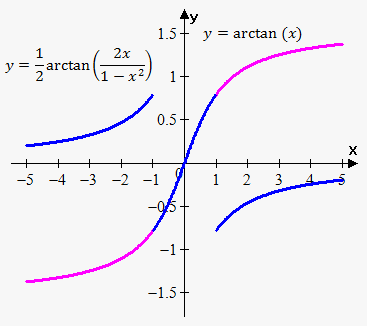 constancy of function

For interval $$${\left(-{1},{1}\right)}$$$ we plug $$${x}={0}$$$: $$$\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}\cdot{0}}}{{{1}-{{0}}^{{2}}}}\right)}}}={\operatorname{arctan}{{\left({0}\right)}}}+{C}$$$ or $$${C}={0}$$$.

For interval $$${\left(-\infty,-{1}\right)}$$$ we let $$${x}\to-\infty$$$: $$${0}=-\frac{\pi}{{2}}+{C}$$$ or $$${C}=\frac{\pi}{{2}}$$$.

For interval $$${\left({1},\infty\right)}$$$ we let $$${x}\to\infty$$$: $$${0}=\frac{\pi}{{2}}+{C}$$$ or $$${C}=-\frac{\pi}{{2}}$$$.

So,

$$$\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}{x}}}{{{1}-{{x}}^{{2}}}}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}+\frac{\pi}{{2}}$$$ on $$${\left(-\infty,-{1}\right)}$$$,

$$$\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}{x}}}{{{1}-{{x}}^{{2}}}}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}$$$ on $$${\left(-{1},{1}\right)}$$$,

$$$\frac{{1}}{{2}}{\operatorname{arctan}{{\left(\frac{{{2}{x}}}{{{1}-{{x}}^{{2}}}}\right)}}}={\operatorname{arctan}{{\left({x}\right)}}}-\frac{\pi}{{2}}$$$ on $$${\left({1},\infty\right)}$$$.

Graph confirms these facts.