One-Sided Limits
Now we can extend concept of limit.
Definition. We write that $$$\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}={L}$$$ and say "the limit of f(x), as x approaches a from the left, equals L" if for any $$$\epsilon>{0}$$$ there exists $$$\delta>{0}$$$ such that $$${\left|{f{{\left({x}\right)}}}-{L}\right|}<\epsilon$$$ when $$${\left|{x}-{a}\right|}<\delta$$$ and $$${x}>{a}$$$.
In other words we are interested in behavior of function near $$${a}$$$ and only to the left from $$${a}$$$.
Definition. We write that $$$\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}={L}$$$ and say "the limit of f(x), as x approaches a from the right, equals L" if for any $$$\epsilon>{0}$$$ there exists $$$\delta>{0}$$$ such that $$${\left|{f{{\left({x}\right)}}}-{L}\right|}<\epsilon$$$ when $$${\left|{x}-{a}\right|}<\delta$$$ and $$${x}<{a}$$$.
In other words we are interested in behavior of function near $$${a}$$$ and only to the right from $$${a}$$$.
One-sided limits often arise for piecewise defined functions.
Example 1. Find $$$\lim_{{{x}\to{{1}}^{+}}}{f{{\left({x}\right)}}}$$$, $$$\lim_{{{x}\to{{1}}^{{-}}}}{f{{\left({x}\right)}}}$$$, $$$\lim_{{{x}\to{1}}}{f{{\left({x}\right)}}}$$$ where $$${f{{\left({x}\right)}}}={\left\{\begin{array}{c}{2}{\quad\text{if}\quad}{x}\ge{1}\\{1}{\quad\text{if}\quad}{x}<{1}\\ \end{array}\right.}$$$.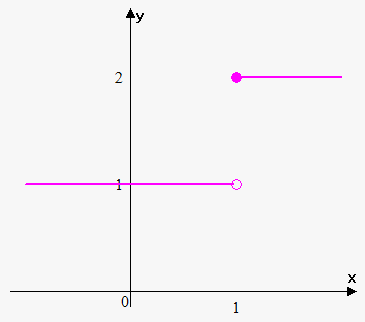
As $$${x}$$$ approaches 1 from the left $$${f{{\left({x}\right)}}}$$$ approaches 1, thus $$$\lim_{{{x}\to{{1}}^{{-}}}}{f{{\left({x}\right)}}}={1}$$$.
As $$${x}$$$ approaches 1 from the right $$${f{{\left({x}\right)}}}$$$ approaches 2, thus $$$\lim_{{{x}\to{{1}}^{+}}}{f{{\left({x}\right)}}}={2}$$$.
So, there is no single number that $$${f{{\left({x}\right)}}}$$$ approaches as $$${x}$$$ approaches 1, thus $$$\lim_{{{x}\to{1}}}{f{{\left({x}\right)}}}$$$ doesn't exist.
Fact. $$$\lim_{{{x}\to{a}}}{f{{\left({x}\right)}}}={L}$$$ if and only if $$$\lim_{{{x}\to{{a}}^{{-}}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{a}}^{+}}}{f{{\left({x}\right)}}}={L}$$$.
This fact is quite useful because often it is easier to find one-sided limits and to check whether they are equal to make conclusion about limit.
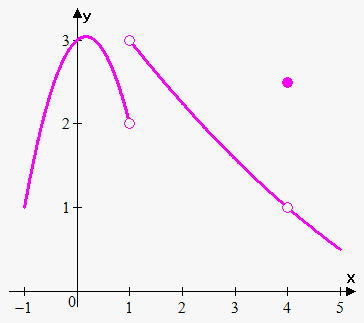
Example 2. The graph of the function $$${f{{\left({x}\right)}}}$$$ is shown. Find (if they exist) values of the following limits:
- $$$\lim_{{{x}\to{{1}}^{{-}}}}{f{{\left({x}\right)}}}$$$
- $$$\lim_{{{x}\to{{1}}^{+}}}{f{{\left({x}\right)}}}$$$
- $$$\lim_{{{x}\to{1}}}{f{{\left({x}\right)}}}$$$
- $$$\lim_{{{x}\to{{4}}^{{-}}}}{f{{\left({x}\right)}}}$$$
- $$$\lim_{{{x}\to{4}+}}{f{{\left({x}\right)}}}$$$
- $$$\lim_{{{x}\to{4}}}{f{{\left({x}\right)}}}$$$
From graph it is seen that $$${f{{\left({x}\right)}}}$$$ approaches 2 as $$${x}$$$ approaches 1 from the left and $$${f{{\left({x}\right)}}}$$$ approaches 3 when $$${x}$$$ approaches 1 from the right.
Therefore, $$$\lim_{{{x}\to{{1}}^{{-}}}}{f{{\left({x}\right)}}}={2}$$$ and $$$\lim_{{{x}\to{{1}}^{+}}}{f{{\left({x}\right)}}}={3}$$$.
Since $$$\lim_{{{x}\to{{1}}^{{-}}}}{f{{\left({x}\right)}}}\ne\lim_{{{x}\to{{1}}^{+}}}{f{{\left({x}\right)}}}$$$ then $$$\lim_{{{x}\to{1}}}{f{{\left({x}\right)}}}$$$ doesn't exist.
Also from graph it can be seen that $$${f{{\left({x}\right)}}}$$$ approaches 1 as $$${x}$$$ approaches 4 from the left and $$${f{{\left({x}\right)}}}$$$ approaches 1 when $$${x}$$$ approaches 4 from the right. Therefore, $$$\lim_{{{x}\to{{4}}^{{-}}}}{f{{\left({x}\right)}}}={1}$$$ and $$$\lim_{{{x}\to{{4}}^{+}}}{f{{\left({x}\right)}}}={1}$$$.
Since $$$\lim_{{{x}\to{{4}}^{{-}}}}{f{{\left({x}\right)}}}=\lim_{{{x}\to{{4}}^{+}}}{f{{\left({x}\right)}}}={1}$$$ then $$$\lim_{{{x}\to{4}}}{f{{\left({x}\right)}}}={1}$$$.
Despite this fact notice that $$${f{{\left({4}\right)}}}\ne{1}$$$.
Example 3. Find $$$\lim_{{{x}\to{0}}}{\left|{x}\right|}$$$.
Recall that $$${\left|{x}\right|}={\left\{\begin{array}{c}{x}{\quad\text{if}\quad}{x}\ge{0}\\-{x}{\quad\text{if}\quad}{x}<{0}\\ \end{array}\right.}$$$.
Therefore, for $$${x}>{0}$$$ $$${\left|{x}\right|}={x}$$$, thus $$$\lim_{{{x}\to{0}+}}{\left|{x}\right|}=\lim_{{{x}\to{{0}}^{+}}}{x}={0}$$$.
Since for $$${x}<{0}$$$ $$${\left|{x}\right|}=-{x}$$$, then $$$\lim_{{{x}\to{{0}}^{{-}}}}{\left|{x}\right|}=\lim_{{{x}\to{{0}}^{{-}}}}-{x}={0}$$$.
We see that $$$\lim_{{{x}\to{{0}}^{+}}}{\left|{x}\right|}=\lim_{{{x}\to{{0}}^{{-}}}}{\left|{x}\right|}={0}$$$. That's why $$$\lim_{{{x}\to{0}}}{\left|{x}\right|}={0}$$$.
Example 4. Find $$$\lim_{{{x}\to{0}}}\frac{{{\left|{x}\right|}}}{{x}}$$$.
For $$${x}>{0}$$$ $$${\left|{x}\right|}={x}$$$, thus $$$\lim_{{{x}\to{0}+}}\frac{{{\left|{x}\right|}}}{{x}}=\lim_{{{x}\to{{0}}^{+}}}\frac{{x}}{{x}}=\lim_{{{x}\to{{0}}^{+}}}{1}={1}$$$.
For $$${x}<{0}$$$ $$${\left|{x}\right|}=-{x}$$$, thus $$$\lim_{{{x}\to{{0}}^{{-}}}}\frac{{{\left|{x}\right|}}}{{x}}=\lim_{{{x}\to{{0}}^{{-}}}}\frac{{-{x}}}{{x}}=\lim_{{{x}\to{{0}}^{{-}}}}-{1}=-{1}$$$.
We see that $$$\lim_{{{x}\to{{0}}^{+}}}\frac{{{\left|{x}\right|}}}{{x}}\ne\lim_{{{x}\to{{0}}^{{-}}}}\frac{{{\left|{x}\right|}}}{{x}}$$$. That's why $$$\lim_{{{x}\to{0}}}\frac{{{\left|{x}\right|}}}{{x}}$$$ doesn't exist.
