1. Home
  2. Math Notes
  3. Calculus I
  4. Creating New Functions from Old

Composition of Functions

Suppose that y=f(u)=ln⁡(u){y}={f{{\left({u}\right)}}}={\ln{{\left({u}\right)}}} and u=g(x)=sin⁡(x){u}={g{{\left({x}\right)}}}={\sin{{\left({x}\right)}}}. Since y{y} is a function of u{u} and u{u} is afunction of x{x} the we obtain that y{y} is a function of x{x}: y=f(u)=f(g(x))=f(sin⁡(x))=ln⁡(sin⁡(x)){y}={f{{\left({u}\right)}}}={f{{\left({g{{\left({x}\right)}}}\right)}}}={f{{\left({\sin{{\left({x}\right)}}}\right)}}}={\ln{{\left({\sin{{\left({x}\right)}}}\right)}}}.

The procedure is called composition because the new function is composed of the two given functions f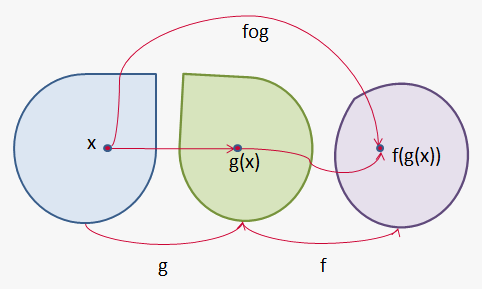f and gg.composition of functions

If we are given two functions ff and gg, we start with a number xx in the domain of gg and find value g(x)g\left(x\right). If this number is in the domain of ff, then we can calculate the value of f(g(x)){f{{\left({g{{\left({x}\right)}}}\right)}}}. The result is a new function h(x)=f(g(x)){h}{\left({x}\right)}={f{{\left({g{{\left({x}\right)}}}\right)}}} obtained by substituting gg into ff.

Definition. Given two functions f{f{}} and g{g{}}, the composite function f∘g{f{\circ}}{g{}} is defined by (f∘g)(x)=f(g(x)){\left({f{\circ}}{g}\right)}{\left({x}\right)}={f{{\left({g{{\left({x}\right)}}}\right)}}}.

Domain of composite functions is set of all x{x} such that x{x} is in domain of g{g{}} and g(x){g{{\left({x}\right)}}} is in domain of f{f{}}.

Example 1. Find f∘g{f{\circ}}{g{}}, g∘f{g{\circ}}{f{}}, f∘f{f{\circ}}{f{}}, g∘g{g{\circ}}{g{}} if f(x)=x3{f{{\left({x}\right)}}}={{x}}^{{3}} and g(x)=xx−1{g{{\left({x}\right)}}}=\frac{\sqrt{{{x}}}}{{{x}-{1}}}.

f∘g=f(g(x))=f(xx−1)=(xx−1)3{f{\circ}}{g{=}}{f{{\left({g{{\left({x}\right)}}}\right)}}}={f{{\left(\frac{\sqrt{{{x}}}}{{{x}-{1}}}\right)}}}={{\left(\frac{\sqrt{{{x}}}}{{{x}-{1}}}\right)}}^{{3}}

g∘f=g(f(x))=g(x3)=x3x3−1{g{\circ}}{f{=}}{g{{\left({f{{\left({x}\right)}}}\right)}}}={g{{\left({{x}}^{{3}}\right)}}}=\frac{\sqrt{{{{x}}^{{3}}}}}{{{{x}}^{{3}}-{1}}}.

Notice, that in general f∘g≠g∘f{f{\circ}}{g{\ne}}{g{\circ}}{f{}}.

f∘f=f(f(x))=f(x3)=(x3)3=x9{f{\circ}}{f{=}}{f{{\left({f{{\left({x}\right)}}}\right)}}}={f{{\left({{x}}^{{3}}\right)}}}={{\left({{x}}^{{3}}\right)}}^{{3}}={{x}}^{{9}}

g∘g=g(g(x))=g(xx−1)=xx−1xx−1−1{g{\circ}}{g{=}}{g{{\left({g{{\left({x}\right)}}}\right)}}}={g{{\left(\frac{\sqrt{{{x}}}}{{{x}-{1}}}\right)}}}=\frac{\sqrt{{\frac{\sqrt{{{x}}}}{{{x}-{1}}}}}}{{\frac{\sqrt{{{x}}}}{{{x}-{1}}}-{1}}}.

Note, that we can take composition of more than two functions: (f∘g∘h)(x)=f(g(h(x))){\left({f{\circ}}{g{\circ}}{h}\right)}{\left({x}\right)}={f{{\left({g{{\left({h}{\left({x}\right)}\right)}}}\right)}}}.

Example 2. Find f∘g∘h{f{\circ}}{g{\circ}}{h} if f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}, g(x)=xx−1{g{{\left({x}\right)}}}=\frac{{x}}{{{x}-{1}}} and h(x)=sin⁡(x){h}{\left({x}\right)}={\sin{{\left({x}\right)}}}.

f∘g∘h=f(g(h(x)))=f(g(sin⁡(x)))=f(sin⁡(x)sin⁡(x)−1)=(sin⁡(x)sin⁡(x)−1)2{f{\circ}}{g{\circ}}{h}={f{{\left({g{{\left({h}{\left({x}\right)}\right)}}}\right)}}}={f{{\left({g{{\left({\sin{{\left({x}\right)}}}\right)}}}\right)}}}={f{{\left(\frac{{\sin{{\left({x}\right)}}}}{{{\sin{{\left({x}\right)}}}-{1}}}\right)}}}={{\left(\frac{{\sin{{\left({x}\right)}}}}{{{\sin{{\left({x}\right)}}}-{1}}}\right)}}^{{2}}.

Sometimes we need to perform inverse task, in other words given composite function, we need to find functions it is formed from.

Example 3. Find f, g, and h if f∘g∘h=(cos⁡(x+9))2{f{\circ}}{g{\circ}}{h}={{\left({\cos{{\left({x}+{9}\right)}}}\right)}}^{{2}}.

The formula for f∘g∘h{f{\circ}}{g{\circ}}{h} says: first add 9, then take the cosine of the result, and finally square.

So, we take h(x)=x+9{h}{\left({x}\right)}={x}+{9}, g(x)=cos⁡(x){g{{\left({x}\right)}}}={\cos{{\left({x}\right)}}} and f(x)=x2{f{{\left({x}\right)}}}={{x}}^{{2}}.

Then

f∘g∘h=f(g(h(x)))=f(g(x+9))=f(cos⁡(x+9))=(cos⁡(x+9))2{f{\circ}}{g{\circ}}{h}={f{{\left({g{{\left({h}{\left({x}\right)}\right)}}}\right)}}}={f{{\left({g{{\left({x}+{9}\right)}}}\right)}}}={f{{\left({\cos{{\left({x}+{9}\right)}}}\right)}}}={{\left({\cos{{\left({x}+{9}\right)}}}\right)}}^{{2}}.

It is worth noting, that characteristic of function as composite is not connected with natural functional dependence of f{f{}} and x{x}, it is just a way to represent this dependence.

For example, let f=1−u2{f{=}}\sqrt{{{1}-{{u}}^{{2}}}} for u∈[−1,1]{u}\in{\left[-{1},{1}\right]} and y=sin⁡(x){y}={\sin{{\left({x}\right)}}} for x∈[−π2,π2]{x}\in{\left[-\frac{\pi}{{2}},\frac{\pi}{{2}}\right]} then (f∘g)(x)=f(g(x))=f(sin⁡(x))=1−(sin⁡(x))2=cos⁡(x){\left({f{\circ}}{g}\right)}{\left({x}\right)}={f{{\left({g{{\left({x}\right)}}}\right)}}}={f{{\left({\sin{{\left({x}\right)}}}\right)}}}=\sqrt{{{1}-{{\left({\sin{{\left({x}\right)}}}\right)}}^{{2}}}}={\cos{{\left({x}\right)}}}. Here cos⁡(x){\cos{{\left({x}\right)}}} is represented as composite function.