1. Home
  2. Math Notes
  3. Calculus I
  4. Applications of Derivatives

Tangent Line to Parametric Curves

Related calculator: Tangent Line Calculator

Sometimes function is defined parametrically, but we still need to find equation of tangent line.

So, let parametric curve is defined by equations x=f(t)x=f{{\left({t}\right)}} and y=g(t)y=g{{\left({t}\right)}}.

Suppose ff and gg are differentiable functions and we want to find the tangent line at a point on the curve where yy is also a differentiable function of xx.

Then using Chain Rule we can write dydt=dydxdxdt\frac{{{d}{y}}}{{{d}{t}}}=\frac{{{d}{y}}}{{{d}{x}}}\frac{{{d}{x}}}{{{d}{t}}}.

If dxdt≠0\frac{{{d}{x}}}{{{d}{t}}}\ne{0} then we solve for dydx\frac{{{d}{y}}}{{{d}{x}}}:

dydx=dydtdxdt{\color{red}{{\frac{{{d}{y}}}{{{d}{x}}}=\frac{{\frac{{{d}{y}}}{{{d}{t}}}}}{{\frac{{{d}{x}}}{{{d}{t}}}}}}}}.

This equation allows us to find the slope dydx\frac{{{d}{y}}}{{{d}{x}}} of tangent line without having to eliminate parameter t{t}.

We see from equation that the curve has

  • horizontal tangent when dydt=0\frac{{{d}{y}}}{{{d}{t}}}={0} (provided that dxdt≠0\frac{{{d}{x}}}{{{d}{t}}}\ne{0}).
  • vertical tangent when dxdt=0\frac{{{d}{x}}}{{{d}{t}}}={0} (provided that dydt≠0\frac{{{d}{y}}}{{{d}{t}}}\ne{0}).

Example 1. Find equation of tangent line at point (5,-1) to the curve x=3t4+t2+1{x}={3}{{t}}^{{4}}+{{t}}^{{2}}+{1} and y=t5−2t{y}={{t}}^{{5}}-{2}{t}. Where curve has horizontal and vertical tangents?

dxdt=3⋅4t4−1+2⋅t2−1=12t3+2t\frac{{{d}{x}}}{{{d}{t}}}={3}\cdot{4}{{t}}^{{{4}-{1}}}+{2}\cdot{{t}}^{{{2}-{1}}}={12}{{t}}^{{3}}+{2}{t}.

dydt=5⋅t5−1−2⋅1t1−1=5t4−2\frac{{{d}{y}}}{{{d}{t}}}={5}\cdot{{t}}^{{{5}-{1}}}-{2}\cdot{1}{{t}}^{{{1}-{1}}}={5}{{t}}^{{4}}-{2}.

At the point with parameter value t, the slope is

dydx=dydtdxdt=5t4−212t3+2t\frac{{{d}{y}}}{{{d}{x}}}=\frac{{\frac{{{d}{y}}}{{{d}{t}}}}}{{\frac{{{d}{x}}}{{{d}{t}}}}}=\frac{{{5}{{t}}^{{4}}-{2}}}{{{12}{{t}}^{{3}}+{2}{t}}}.

Point (5,-1) corresponds to t=1{t}={1}, so dydx∣t=1=5⋅14−212⋅13+2⋅1=314\frac{{{d}{y}}}{{{d}{x}}}{\mid}_{{{t}={1}}}=\frac{{{5}\cdot{{1}}^{{4}}-{2}}}{{{12}\cdot{{1}}^{{3}}+{2}\cdot{1}}}=\frac{{3}}{{14}}.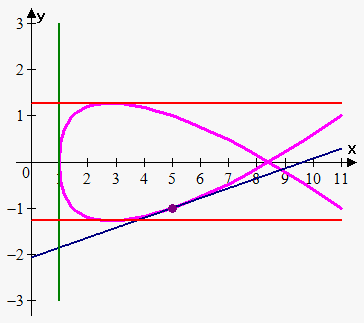tangent line to parametric curve

Therefore, equation of tangent line is y+1=314(x−5){y}+{1}=\frac{{3}}{{14}}{\left({x}-{5}\right)} or y=314x−2914{y}=\frac{{3}}{{14}}{x}-\frac{{29}}{{14}} (blue line).

Curve has horizontal tangent when dydt=0\frac{{{d}{y}}}{{{d}{t}}}={0} or 5t4−2=0{5}{{t}}^{{4}}-{2}={0}. So, tangent line is horizontal at t=±254≈±0.795271{t}=\pm{\sqrt[{{4}}]{{\frac{{2}}{{5}}}}}\approx\pm{0.795271}.

When t=0.795271{t}={0.795271} (x,y)=(1.8324576,−1.272433){\left({x},{y}\right)}={\left({1.8324576},-{1.272433}\right)}.

When t=−0.795271{t}=-{0.795271} (x,y)=(1.8324576,1.272433){\left({x},{y}\right)}={\left({1.8324576},{1.272433}\right)}.

Curve has vertical tangent when dxdt=0\frac{{{d}{x}}}{{{d}{t}}}={0} or 12t3+2t=0{12}{{t}}^{{3}}+{2}{t}={0}. So, tangent line is horizontal at t=0{t}={0}.

When t=0{t}={0} (x,y)=(0,0){\left({x},{y}\right)}={\left({0},{0}\right)}.

As appears from graph our answers are correct (green line is vertical tangent, red lines are horizontal tangents).

Finally, let's see example when there can be more than one tangent line at point.

Example 2. Find equation of tangent line to x=t2{x}={{t}}^{{2}}, y=t3−4t{y}={{t}}^{{3}}-{4}{t} at point (4,0){\left({4},{0}\right)}.

First let's find values of t{t} for which x=4{x}={4} and y=0{y}={0}.

So, t2=4{{t}}^{{2}}={4} when t=±2{t}=\pm{2} and t3−4t=t(t2−4)=0{{t}}^{{3}}-{4}{t}={t}{\left({{t}}^{{2}}-{4}\right)}={0} when t=0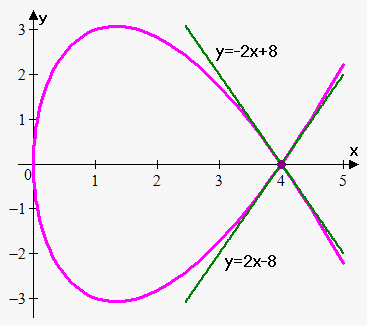{t}={0} and t=±2{t}=\pm{2}.two tangent lines to parametric curve at one point

So, x=4{x}={4}, y=0{y}={0} when t=±2{t}=\pm{2}. Note that we obtained two values for t{t}, so there will be two tangent lines.

Now, let's find derivative:

dydx=dydtdxdt=3t2−42t\frac{{{d}{y}}}{{{d}{x}}}=\frac{{\frac{{{d}{y}}}{{{d}{t}}}}}{{\frac{{{d}{x}}}{{{d}{t}}}}}=\frac{{{3}{{t}}^{{2}}-{4}}}{{{2}{t}}}.

When t=2{t}={2} we have that dydx∣t=2=3⋅22−42⋅2=2\frac{{{d}{y}}}{{{d}{x}}}{\mid}_{{{t}={2}}}=\frac{{{3}\cdot{{2}}^{{2}}-{4}}}{{{2}\cdot{2}}}={2}.

So, first tangent line is y−0=2(x−4){y}-{0}={2}{\left({x}-{4}\right)} or y=2x−8{y}={2}{x}-{8}.

When t=−2{t}=-{2} we have that dydx−∣t=2=3⋅(−2)2−42⋅(−2)=−2\frac{{{d}{y}}}{{{d}{x}}}-{\mid}_{{{t}={2}}}=\frac{{{3}\cdot{{\left(-{2}\right)}}^{{2}}-{4}}}{{{2}\cdot{\left(-{2}\right)}}}=-{2}.

Thus, second tangent line is y−0=−2(x−4){y}-{0}=-{2}{\left({x}-{4}\right)} or y=−2x+8{y}=-{2}{x}+{8}.

As can be seen there are two tangents at point where curve crosses itself, so there are one tangent line for each instance that the curve goes through the point.