Volume of Solid of Revolution about Slant Line
We know how to find the volume of a solid of revolution obtained by rotating a region about a horizontal or vertical line (see Method of Disks/Rings and Method of Cylindrical Shells). But what if we rotate about a slanted line, that is, a line that is neither horizontal nor vertical?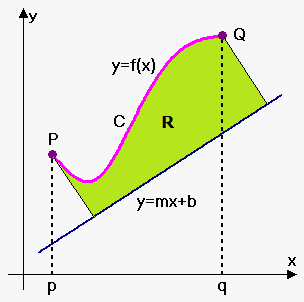
Let $$${C}$$$ be the arc of the curve $$${y}={f{{\left({x}\right)}}}$$$ between the points $$${P}={\left({p},{f{{\left({p}\right)}}}\right)}$$$ and $$${B}={\left({q},{f{{\left({q}\right)}}}\right)}$$$ and let $$${R}$$$ be the region bounded by $$${C}$$$, by the line $$${y}={m}{x}+{b}$$$ (which lies entirely below $$${C}$$$), and by the perpendiculars to the line from $$${A}$$$ and $$${B}$$$.
We first will try to find area of region $$${R}$$$. For this we will need another sketch.
We again approximate area by the sum or rectangles, but this time rectangles are perpendicular to the line $$${y}={m}{x}+{b}$$$. Area of i-th rectangle is $$${L}_{{i}}\Delta{u}$$$. Thus, approximate area of $$${R}$$$ is $$${A}\approx{\sum_{{{i}={1}}}^{{n}}}{L}_{{i}}\Delta{u}$$$.
Taking $$${n}$$$ very large we have that $$${A}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{L}_{{i}}\Delta{u}$$$.
We need to express $$${L}_{{i}}$$$ and $$$\Delta{u}$$$ in terms of $$$\Delta{x}$$$.
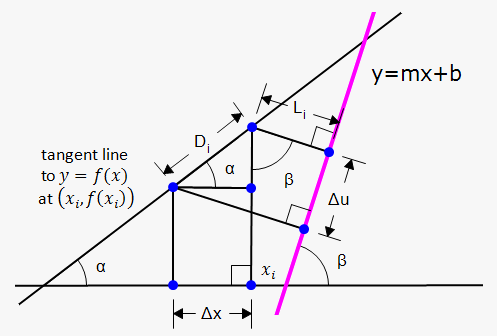
From the sketch we immediately have that $$${\tan{{\left(\alpha\right)}}}={f{'}}{\left({x}_{{i}}\right)}$$$ (slope of tangent line) and $$${\tan{{\left(\beta\right)}}}={m}$$$.
Also, $$${D}_{{i}}=\frac{{\Delta{x}}}{{\cos{{\left(\alpha\right)}}}}$$$, and $$$\Delta{u}={D}_{{i}}{\cos{{\left(\beta-\alpha\right)}}}={D}_{{i}}{\left({\cos{{\left(\beta\right)}}}{\cos{{\left(\alpha\right)}}}+{\sin{{\left(\alpha\right)}}}{\sin{{\left(\beta\right)}}}\right)}$$$.
From this we have that $$$\Delta{u}=\frac{{\Delta{x}}}{{{\cos{{\left(\alpha\right)}}}}}{\left({\cos{{\left(\beta\right)}}}{\cos{{\left(\alpha\right)}}}+{\sin{{\left(\alpha\right)}}}{\sin{{\left(\beta\right)}}}\right)}=\Delta{x}{\left({\cos{{\left(\beta\right)}}}+{\tan{{\left(\alpha\right)}}}{\sin{{\left(\beta\right)}}}\right)}$$$.
Now, we need to express $$${\sin{{\left(\beta\right)}}}$$$ and $$${\cos{{\left(\beta\right)}}}$$$ in terms of $$${\tan{{\left(\beta\right)}}}$$$.
From identity $$${{\tan}}^{{2}}{\left(\beta\right)}+{1}=\frac{{1}}{{{{\cos}}^{{2}}{\left(\beta\right)}}}$$$ we have that $$${\cos{{\left(\beta\right)}}}=\sqrt{{\frac{{1}}{{{1}+{{\tan}}^{{2}}{\left(\beta\right)}}}}}=\sqrt{{\frac{{1}}{{{1}+{{m}}^{{2}}}}}}$$$.
Since $$${{\sin}}^{{2}}{\left(\beta\right)}+{{\cos}}^{{2}}{\left(\beta\right)}={1}$$$ then $$${\sin{{\left(\beta\right)}}}=\frac{{m}}{\sqrt{{{{m}}^{{2}}+{1}}}}$$$.
Therefore, $$$\Delta{u}=\Delta{x}{\left(\frac{{1}}{{\sqrt{{{{m}}^{{2}}+{1}}}}}+{f{'}}{\left({x}_{{i}}\right)}\frac{{m}}{\sqrt{{{{m}}^{{2}}+{1}}}}\right)}=\Delta{x}\frac{{{1}+{m}{f{'}}{\left({x}_{{i}}\right)}}}{{\sqrt{{{{m}}^{{2}}+{1}}}}}$$$.
Now, we need to determine $$${L}_{{i}}$$$.
It is fairly easy to do: $$${L}_{{i}}={\left({f{{\left({x}_{{i}}\right)}}}-{\left({m}{x}_{{i}}+{b}\right)}\right)}{\cos{{\left(\beta\right)}}}=\frac{{{f{{\left({x}_{{i}}\right)}}}-{m}{x}_{{i}}-{b}}}{{\sqrt{{{{m}}^{{2}}+{1}}}}}$$$.
That's all. $$${A}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{L}_{{i}}\Delta{u}=\frac{{{f{{\left({x}_{{i}}\right)}}}-{m}{x}_{{i}}-{b}}}{\sqrt{{{{m}}^{{2}}+{1}}}}\cdot\frac{{{1}+{m}{f{'}}{\left({x}_{{i}}\right)}}}{{\sqrt{{{{m}}^{{2}}+{1}}}}}\Delta{x}=\frac{{1}}{{{{m}}^{{2}}+{1}}}\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{\left({f{{\left({x}_{{i}}\right)}}}-{m}{x}_{{i}}-{b}\right)}{\left({1}+{m}{f{'}}{\left({x}_{{i}}\right)}\right)}$$$.
This is limit of the Riemann sum, i.e. definite integral, so
Area of region R is $$${A}=\frac{{1}}{{{{m}}^{{2}}+{1}}}{\int_{{p}}^{{q}}}{\left({f{{\left({x}\right)}}}-{m}{x}-{b}\right)}{\left({1}+{m}{f{'}}{\left({x}\right)}\right)}{d}{x}$$$.
Now, to find volume we use method of disks: we slice perpendicular to the line $$${y}={m}{x}+{b}$$$: radius of disk is $$${L}=\frac{{{f{{\left({x}\right)}}}-{m}{x}-{b}}}{\sqrt{{{{m}}^{{2}}+{1}}}}$$$.
Thus, $$${A}{\left({x}\right)}=\pi{{L}}^{{2}}=\pi{{\left(\frac{{{f{{\left({x}\right)}}}-{m}{x}-{b}}}{{\sqrt{{{{m}}^{{2}}+{1}}}}}\right)}}^{{2}}$$$.
Therefore, $$${V}={\int_{{p}}^{{q}}}\pi{{L}}^{{2}}{d}{u}={\int_{{p}}^{{q}}}\pi{{\left(\frac{{{f{{\left({x}\right)}}}-{m}{x}-{b}}}{\sqrt{{{{m}}^{{2}}+{1}}}}\right)}}^{{2}}\frac{{{1}+{m}{f{'}}{\left({x}\right)}}}{\sqrt{{{{m}}^{{2}}+{1}}}}{d}{x}$$$.
Volume of Solid of Revolution around Slant Line $$${y}={m}{x}+{b}$$$ is $$${V}=\frac{\pi}{{{\left({{m}}^{{2}}+{1}\right)}}^{{\frac{{3}}{{2}}}}}{\int_{{p}}^{{q}}}{{\left({f{{\left({x}\right)}}}-{m}{x}-{b}\right)}}^{{2}}{\left({1}+{m}{f{'}}{\left({x}\right)}\right)}{d}{x}$$$.
Example. Find the area of region $$${R}$$$ bounded by $$${f{{\left({x}\right)}}}={x}+{\sin{{\left({x}\right)}}}$$$, by the line $$${y}={x}-{2}$$$, and by the perpendiculars to the line from $$${P}={\left({0},{0}\right)}$$$ and $$${Q}={\left({2}\pi,{2}\pi\right)}$$$. Find volume of the solid obtained by rotating the region $$${R}$$$ about the line $$${y}={x}-{2}$$$.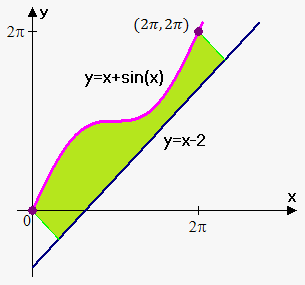
Here we have $$${m}={1}$$$, $$${b}=-{2}$$$, $$${f{{\left({x}\right)}}}={x}+{\sin{{\left({x}\right)}}}$$$, thus, $$${f{'}}{\left({x}\right)}={1}+{\cos{{\left({x}\right)}}}$$$.
Therefore, $$${A}=\frac{{1}}{{{{1}}^{{2}}+{1}}}{\int_{{0}}^{{{2}\pi}}}{\left({x}+{\sin{{\left({x}\right)}}}-{x}+{2}\right)}{\left({1}+{1}\cdot{\left({1}+{\cos{{\left({x}\right)}}}\right)}\right)}{d}{x}=$$$
$$$=\frac{{1}}{{2}}{\int_{{0}}^{{{2}\pi}}}{\left({2}+{\sin{{\left({x}\right)}}}\right)}{\left({2}+{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{{1}}{{2}}{\int_{{0}}^{{{2}\pi}}}{\left({4}+{2}{\cos{{\left({x}\right)}}}+{2}{\sin{{\left({x}\right)}}}+{\sin{{\left({x}\right)}}}{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{{1}}{{2}}{\int_{{0}}^{{{2}\pi}}}{\left({4}+{2}{\cos{{\left({x}\right)}}}+{2}{\sin{{\left({x}\right)}}}+\frac{{1}}{{2}}{\sin{{\left({2}{x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{{1}}{{2}}{\left({4}{x}+{2}{\sin{{\left({x}\right)}}}-{2}{\cos{{\left({x}\right)}}}-\frac{{1}}{{4}}{\cos{{\left({2}{x}\right)}}}\right)}{{\mid}_{{0}}^{{{2}\pi}}}=\frac{{1}}{{2}}{\left({8}\pi-{2}-\frac{{1}}{{4}}+{2}+\frac{{1}}{{4}}\right)}={4}\pi$$$.
And volume is
$$${V}=\frac{\pi}{{{\left({{1}}^{{2}}+{1}\right)}}^{{\frac{{3}}{{2}}}}}{\int_{{0}}^{{{2}\pi}}}{{\left({x}+{\sin{{\left({x}\right)}}}-{x}+{2}\right)}}^{{2}}{\left({1}+{1}\cdot{\left({1}+{\cos{{\left({x}\right)}}}\right)}\right)}{d}{x}=\frac{\pi}{\sqrt{{{8}}}}{\int_{{0}}^{{{2}\pi}}}{{\left({2}+{\sin{{\left({x}\right)}}}\right)}}^{{2}}{\left({2}+{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{\pi}{\sqrt{{{8}}}}{\int_{{0}}^{{{2}\pi}}}{\left({4}+{4}{\sin{{\left({x}\right)}}}+{{\sin}}^{{2}}{\left({x}\right)}\right)}{\left({2}+{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{\pi}{\sqrt{{{8}}}}{\int_{{0}}^{{{2}\pi}}}{\left({8}+{4}{\cos{{\left({x}\right)}}}+{8}{\sin{{\left({x}\right)}}}+{4}{\sin{{\left({x}\right)}}}{\cos{{\left({x}\right)}}}+{2}{{\sin}}^{{2}}{\left({x}\right)}+{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}\right)}{d}{x}$$$
Now we use double angle formulas and integral can be rewritten as
$$$=\frac{\pi}{\sqrt{{{8}}}}{\int_{{0}}^{{{2}\pi}}}{\left({8}+{4}{\cos{{\left({x}\right)}}}+{8}{\sin{{\left({x}\right)}}}+{2}{\sin{{\left({2}{x}\right)}}}+{1}-{\cos{{\left({2}{x}\right)}}}+{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{\pi}{\sqrt{{{8}}}}{\int_{{0}}^{{{2}\pi}}}{\left({9}+{4}{\cos{{\left({x}\right)}}}+{8}{\sin{{\left({x}\right)}}}+{2}{\sin{{\left({2}{x}\right)}}}-{\cos{{\left({2}{x}\right)}}}+{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}\right)}{d}{x}=$$$
$$$=\frac{\pi}{\sqrt{{{8}}}}{\left({9}{x}+{4}{\sin{{\left({x}\right)}}}-{8}{\cos{{\left({x}\right)}}}-{\cos{{\left({2}{x}\right)}}}-\frac{{1}}{{2}}{\sin{{\left({2}{x}\right)}}}+\frac{{1}}{{3}}{{\sin}}^{{3}}{\left({x}\right)}\right)}{{\mid}_{{0}}^{{{2}\pi}}}=$$$
$$$=\frac{\pi}{\sqrt{{{8}}}}{\left({18}\pi-{8}-{1}+{8}+{1}\right)}=\frac{\pi}{\sqrt{{{8}}}}\cdot{18}\pi=\frac{{{9}{\pi}^{{2}}}}{\sqrt{{{2}}}}$$$.
Note, how we used substitution $$${u}={\sin{{\left({x}\right)}}}$$$ for integral $$$\int{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}{d}{x}$$$ to obtain that $$$\int{{\sin}}^{{2}}{\left({x}\right)}{\cos{{\left({x}\right)}}}{d}{x}=\frac{{1}}{{3}}{{\sin}}^{{3}}{\left({x}\right)}{d}{x}$$$.
