Consumer and Producer Surpluses

Economists often use demand function $$${D}{\left({p}\right)}$$$. The demand function $$${D}{\left({p}\right)}$$$ is the quantity of goods that can be sold when price of 1 unit is $$${p}$$$. Usually, the bigger price, the lower demand, so the demand function is a decreasing function.

Also economists use supply function $$${S}{\left({p}\right)}$$$. The supply function $$${S}{\left({p}\right)}$$$ is the quantity of goods that are supplied when price of 1 unit is $$${p}$$$. Usually, the bigger price, the higher supply, so the supply function is an increasing function.

When supply and demand are equalthe economy is said to be at equilibrium. At this point (point $$${\left({{P}}^{\star},{{Q}}^{\star}\right)}$$$), the allocation of goods is most efficient because the amount of goods being supplied is exactly the same as the amount of goods being demanded. At the equilibrium price suppliers are selling all the goods that they have produced and consumers are getting all the goods that they are demanding.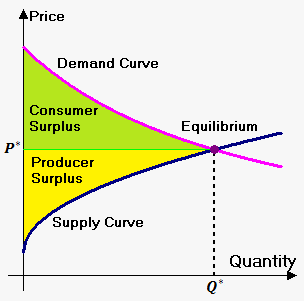

Consumer surplus is the amount of money saved by consumers because they are able to purchase a product for a price that is less than the highest price that they would be willing to pay.

Consumer surplus is the area under the demand curve and above the line $$${p}={{P}}^{\star}$$$.

Producer surplus is the amount that producers benefit by selling products at price $$${{P}}^{\star}$$$ that is higher than the least that they would be willing to sell for.

Producer surplus is area above supply curve and below the line $$${p}={{P}}^{\star}$$$.

Example. A demand curve is given by $$${D}=\frac{{450}}{{{p}+{8}}}$$$ and supply curve is given by $$${S}={p}+{49}$$$. Find the consumer and producer surpluses.

We first must find equilibrium points. For this solve equation $$${D}={S}$$$.

So, $$$\frac{{450}}{{{p}+{8}}}={p}+{49}$$$ or $$${\left({p}+{49}\right)}{\left({p}+{8}\right)}={450}$$$.

From this we obtain quadratic equation $$${{p}}^{{2}}+{57}{p}-{58}={0}$$$. Its roots are $$${p}={1}$$$ and $$${p}=-{58}$$$.

Price can't be negative, so the only equlibrium price is $$${{P}}^{\star}={1}$$$. Corresponding quantity is $$${{Q}}^{\star}={1}+{49}={50}$$$.

Now, consumer surplus is area under demand curve on interval $$${\left[{0},{{P}}^{\star}\right]}$$$ minus area of rectangle $$${{P}}^{\star}\cdot{{Q}}^{\star}$$$: $$${C}{S}={\int_{{0}}^{{1}}}\frac{{450}}{{{x}+{8}}}{d}{x}-{1}\cdot{50}={450}{\ln{{\left({x}+{8}\right)}}}{{\mid}_{{0}}^{{1}}}-{50}={450}{\left({\ln{{\left({9}\right)}}}-{\ln{{\left({8}\right)}}}\right)}-{50}\approx{3}\$$$$.

Producer surplus is area under rectangle minus area below supply curve on interval $$${\left[{0},{{P}}^{\star}\right]}$$$: $$${P}{S}={1}\cdot{50}-{\int_{{0}}^{{1}}}{\left({x}+{49}\right)}{d}{x}={50}-{\left(\frac{{1}}{{2}}{{x}}^{{2}}+{49}{x}\right)}{{\mid}_{{0}}^{{1}}}=\frac{{1}}{{2}}$$$.