1. Home
  2. Math Notes
  3. Calculus II
  4. Applications of Integrals

Area in Polar Coordinates

To find area in polar coordinates of curve on interval [a,b]{\left[{a},{b}\right]} we use same idea as in calculating area in rectangular coordinates.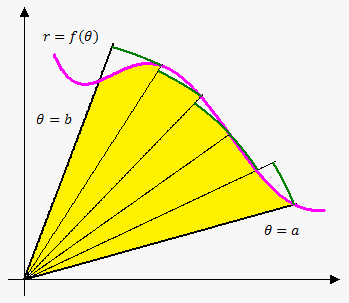area in polar coordinates

So, consider region, that is bounded by θ=a\theta={a}, θ=b\theta={b} and curve r=f(θ){r}={f{{\left(\theta\right)}}}.

We divide this region into n{n} subintervals of length Δθ=b−an\Delta\theta=\frac{{{b}-{a}}}{{n}}.

Now choose in each interval [θi−1,θ]{\left[\theta_{{{i}-{1}}},\theta\right]} sample point θi⋆{\theta_{{i}}^{\star}} (on the figure we chose right endpoint) and approximate area on i-th subinterval by area of sector whose radius is r(θi⋆){r}{\left({\theta_{{i}}^{\star}}\right)}: Ai=Δθ2π⋅π(r(θi⋆))2{A}_{{i}}=\frac{{\Delta\theta}}{{{2}\pi}}\cdot\pi{{\left({r}{\left({\theta_{{i}}^{\star}}\right)}\right)}}^{{2}}.

Summing these area we will obtain that required area is A≈∑i=1n12(r(θi⋆))2Δθ{A}\approx{\sum_{{{i}={1}}}^{{n}}}\frac{{1}}{{2}}{{\left({r}{\left({\theta_{{i}}^{\star}}\right)}\right)}}^{{2}}\Delta\theta.

If we let n→∞{n}\to\infty then we obtain exact area A=lim⁡n→∞∑i=1n12(r(θi⋆))2Δθ{A}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}\frac{{1}}{{2}}{{\left({r}{\left({\theta_{{i}}^{\star}}\right)}\right)}}^{{2}}\Delta\theta.

We recognize in this sum Riemann sum, so A{A} can be found using integral.

Area in Polar Coordinates. A=12∫ab(r(θ))2dθ{A}=\frac{{1}}{{2}}{\int_{{a}}^{{b}}}{{\left({r}{\left(\theta\right)}\right)}}^{{2}}{d}\theta.

Example 1. Determine area of the inner loop of the r=1+2sin⁡(θ){r}={1}+{2}{\sin{{\left(\theta\right)}}}.

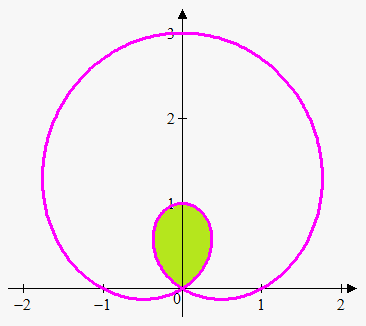area in polar coordinates enclosed by one curveTo handle this problem we need bound for inner loop. Loop starts at the origin and ends at the origin, so we need points where 1+2sin⁡(θ)=0{1}+{2}{\sin{{\left(\theta\right)}}}={0}. Solving this equation on interval [0,2π]{\left[{0},{2}\pi\right]} we obtain that θ=7π6\theta=\frac{{{7}\pi}}{{6}} and θ=11π6\theta=\frac{{{11}\pi}}{{6}}.

So, A=12∫7π611π6(1+2sin⁡(θ))2dθ={A}=\frac{{1}}{{2}}{\int_{{\frac{{{7}\pi}}{{6}}}}^{{\frac{{{11}\pi}}{{6}}}}}{{\left({1}+{2}{\sin{{\left(\theta\right)}}}\right)}}^{{2}}{d}\theta=

=12∫7π611π6(1+4sin⁡(θ)+4sin⁡2(θ))dθ==\frac{{1}}{{2}}{\int_{{\frac{{{7}\pi}}{{6}}}}^{{\frac{{{11}\pi}}{{6}}}}}{\left({1}+{4}{\sin{{\left(\theta\right)}}}+{4}{{\sin}}^{{2}}{\left(\theta\right)}\right)}{d}\theta=

=12∫7π611π6(1+4sin⁡(θ)+2(1−cos⁡(2θ)))dθ=12(3θ−4cos⁡(θ)−sin⁡(2θ))∣7π611π6=π−332=\frac{{1}}{{2}}{\int_{{\frac{{{7}\pi}}{{6}}}}^{{\frac{{{11}\pi}}{{6}}}}}{\left({1}+{4}{\sin{{\left(\theta\right)}}}+{2}{\left({1}-{\cos{{\left({2}\theta\right)}}}\right)}\right)}{d}\theta=\frac{{1}}{{2}}{\left({3}\theta-{4}{\cos{{\left(\theta\right)}}}-{\sin{{\left({2}\theta\right)}}}\right)}{{\mid}_{{\frac{{{7}\pi}}{{6}}}}^{{\frac{{{11}\pi}}{{6}}}}}=\pi-\frac{{{3}\sqrt{{{3}}}}}{{2}}.

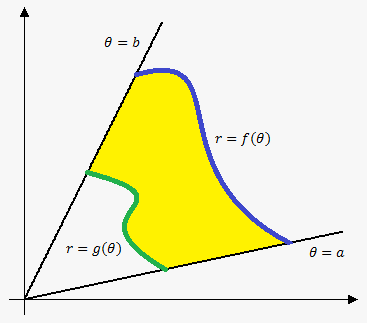area between curves in polar coordinatesSimilarly we can derive formula for area enclosed by two curves. Indeed, if area enclosed by curve r=f(θ){r}={f{{\left(\theta\right)}}} is 12∫ab(f(θ))2dθ\frac{{1}}{{2}}{\int_{{a}}^{{b}}}{{\left({f{{\left(\theta\right)}}}\right)}}^{{2}}{d}\theta, area enclosed by curve r=g(θ){r}={g{{\left(\theta\right)}}} is 12∫ab(g(θ))2dθ\frac{{1}}{{2}}{\int_{{a}}^{{b}}}{{\left({g{{\left(\theta\right)}}}\right)}}^{{2}}{d}\theta and f(θ)≥g(θ){f{{\left(\theta\right)}}}\ge{g{{\left(\theta\right)}}} for a≤θ≤b{a}\le\theta\le{b} then area between them is difference of corresponding areas.

Area Enclosed By Curves in Polar Coordinates. Suppose r=f(θ){r}={f{{\left(\theta\right)}}} and r=g(θ){r}={g{{\left(\theta\right)}}} are two curves in polar coordinates continuous on [a,b]{\left[{a},{b}\right]} and f(θ)≥g(θ){f{{\left(\theta\right)}}}\ge{g{{\left(\theta\right)}}} for a≤θ≤b{a}\le\theta\le{b}, then area enclosed by them is A=12∫ab((f(θ))2−(g(θ))2)dθ{A}=\frac{{1}}{{2}}{\int_{{a}}^{{b}}}{\left({{\left({f{{\left(\theta\right)}}}\right)}}^{{2}}-{{\left({g{{\left(\theta\right)}}}\right)}}^{{2}}\right)}{d}\theta.

Example 2. Consider limacon r=3+2cos⁡(θ){r}={3}+{2}{\cos{{\left(\theta\right)}}} and circle r=2{r}={2}. Find area inside limacon and outside circle, outside limacon and inside circle, inside both limacon and circle.

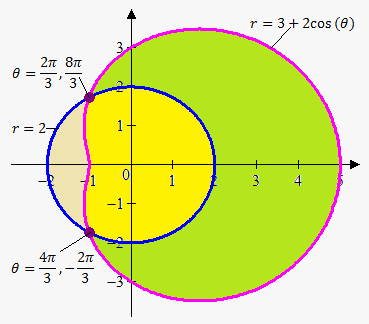area enclosed in polar coordinatesFirst we need to find points of intersection of two graphs: 3+2cos⁡(θ)=2{3}+{2}{\cos{{\left(\theta\right)}}}={2} or cos⁡(θ)=−12{\cos{{\left(\theta\right)}}}=-\frac{{1}}{{2}}. This gives θ=2π3\theta=\frac{{{2}\pi}}{{3}} and θ=4π3\theta=\frac{{{4}\pi}}{{3}}.

So first we need area inside limacon and outside circle (green area).

To enclose area we should move counterclockwise, i.e. from smaller angle to bigger. We encounter problem here. To enclose green are we should move from 4π3\frac{{{4}\pi}}{{3}} to 2π3\frac{{{2}\pi}}{{3}}. But we should move from smaller to greater angle. This means that either we increase smaller angle or decrease greater angle. Luckily, since we are in polar coordinates we can substitute angle θ\theta either by θ+2π\theta+{2}\pi or θ−2π\theta-{2}\pi.

So, either we move from 4π3−2π=−2π3\frac{{{4}\pi}}{{3}}-{2}\pi=-\frac{{{2}\pi}}{{3}} to 2π3\frac{{{2}\pi}}{{3}} or from 4π3\frac{{{4}\pi}}{{3}} to 2π3+2π=8π3\frac{{{2}\pi}}{{3}}+{2}\pi=\frac{{{8}\pi}}{{3}}. We choose first variant.

Also note that limacon is upper bound on this interval, so

A1=12∫−2π32π3((3+2cos⁡(θ))2−22)dθ={A}_{{1}}=\frac{{1}}{{2}}{\int_{{-\frac{{{2}\pi}}{{3}}}}^{{\frac{{{2}\pi}}{{3}}}}}{\left({{\left({3}+{2}{\cos{{\left(\theta\right)}}}\right)}}^{{2}}-{{2}}^{{2}}\right)}{d}\theta=

=12∫−2π32π3(5+12cos⁡(θ)+4cos⁡2(θ))dθ==\frac{{1}}{{2}}{\int_{{-\frac{{{2}\pi}}{{3}}}}^{{\frac{{{2}\pi}}{{3}}}}}{\left({5}+{12}{\cos{{\left(\theta\right)}}}+{4}{{\cos}}^{{2}}{\left(\theta\right)}\right)}{d}\theta=

=12∫−2π32π3(7+12cos⁡(θ)−2cos⁡(2θ))dθ=12(7θ+12sin⁡(θ)−sin⁡(2θ))∣−2π32π3=14π3+1132=\frac{{1}}{{2}}{\int_{{-\frac{{{2}\pi}}{{3}}}}^{{\frac{{{2}\pi}}{{3}}}}}{\left({7}+{12}{\cos{{\left(\theta\right)}}}-{2}{\cos{{\left({2}\theta\right)}}}\right)}{d}\theta=\frac{{1}}{{2}}{\left({7}\theta+{12}{\sin{{\left(\theta\right)}}}-{\sin{{\left({2}\theta\right)}}}\right)}{{\mid}_{{-\frac{{{2}\pi}}{{3}}}}^{{\frac{{{2}\pi}}{{3}}}}}=\frac{{{14}\pi}}{{3}}+\frac{{{11}\sqrt{{{3}}}}}{{2}}.

Now let's find area enclosed outside limacon and inside circle (light brown area). Here we need to use same bounds but move from θ=2π3\theta=\frac{{{2}\pi}}{{3}} to θ=4π3\theta=\frac{{{4}\pi}}{{3}}. So we don't need any shift in angle here.

Also, note that on this interval circle is upper bound, so we will obtain integral that has opposite to previous integral sign and with different bounds, so

A2=12∫2π34π3(22−(3+2cos⁡(θ))2)dθ=12(sin⁡(2θ)−7θ−12sin⁡(θ))∣2π34π3=1132−7π3{A}_{{2}}=\frac{{1}}{{2}}{\int_{{\frac{{{2}\pi}}{{3}}}}^{{\frac{{{4}\pi}}{{3}}}}}{\left({{2}}^{{2}}-{{\left({3}+{2}{\cos{{\left(\theta\right)}}}\right)}}^{{2}}\right)}{d}\theta=\frac{{1}}{{2}}{\left({\sin{{\left({2}\theta\right)}}}-{7}\theta-{12}{\sin{{\left(\theta\right)}}}\right)}{{\mid}_{{\frac{{{2}\pi}}{{3}}}}^{{\frac{{{4}\pi}}{{3}}}}}=\frac{{{11}\sqrt{{{3}}}}}{{2}}-\frac{{{7}\pi}}{{3}}.

Finally, with yellow region we can't apply formula for area anymore, because on different intervals there are different bounds (on interval [−2π3,2π3]{\left[-\frac{{{2}\pi}}{{3}},\frac{{{2}\pi}}{{3}}\right]} upper bound is circle and no lower bound, on interval [2π3,4π3]{\left[\frac{{{2}\pi}}{{3}},\frac{{{4}\pi}}{{3}}\right]} upper bound is limacon and no lower bound).

However, there are 3 methods to find area A3{A}_{{3}} of yellow region.

First method: notice that area of yellow region is area of circle minus area of light brown region: A3=π⋅(2)2−A2=4π−(1132−7π3)=19π3−1132{A}_{{3}}=\pi\cdot{{\left({2}\right)}}^{{2}}-{A}_{{2}}={4}\pi-{\left(\frac{{{11}\sqrt{{{3}}}}}{{2}}-\frac{{{7}\pi}}{{3}}\right)}=\frac{{{19}\pi}}{{3}}-\frac{{{11}\sqrt{{{3}}}}}{{2}}.

Second method: notice that area of yellow region is area of limacon minus area of green region: A3=12∫02π(3+2cos⁡(θ))2dθ−A1=11π−(14π3+1132)=19π3−1132{A}_{{3}}=\frac{{1}}{{2}}{\int_{{0}}^{{{2}\pi}}}{{\left({3}+{2}{\cos{{\left(\theta\right)}}}\right)}}^{{2}}{d}\theta-{A}_{{1}}={11}\pi-{\left(\frac{{{14}\pi}}{{3}}+\frac{{{11}\sqrt{{{3}}}}}{{2}}\right)}=\frac{{{19}\pi}}{{3}}-\frac{{{11}\sqrt{{{3}}}}}{{2}}.

Third method: integrate on each interval with different upper bounds as was stated above using formula for area with one function:

A3=12∫−2π32π322dθ+12∫2π34π3(3+2cos⁡(θ))2dθ=8π3+(11π3−1132)=19π3−1132{A}_{{3}}=\frac{{1}}{{2}}{\int_{{-\frac{{{2}\pi}}{{3}}}}^{{\frac{{{2}\pi}}{{3}}}}}{{2}}^{{2}}{d}\theta+\frac{{1}}{{2}}{\int_{{\frac{{{2}\pi}}{{3}}}}^{{\frac{{{4}\pi}}{{3}}}}}{{\left({3}+{2}{\cos{{\left(\theta\right)}}}\right)}}^{{2}}{d}\theta=\frac{{{8}\pi}}{{3}}+{\left(\frac{{{11}\pi}}{{3}}-\frac{{{11}\sqrt{{{3}}}}}{{2}}\right)}=\frac{{{19}\pi}}{{3}}-\frac{{{11}\sqrt{{{3}}}}}{{2}}.