Inverse Trigonometric Functions

Clearly all trigonometric functions due to periodicity fail horizontal line test. Therefore, they don't have inverse. But if we consider interval where piece of function passes horizontal line test and takes all values from its range, then we can find inverse function.

For function $$${y}={\sin{{\left({x}\right)}}}$$$ we take interval $$${\left[-\frac{\pi}{{2}},\frac{\pi}{{2}}\right]}$$$. Function takes all values from range $$${\left[-{1},{1}\right]}$$$ 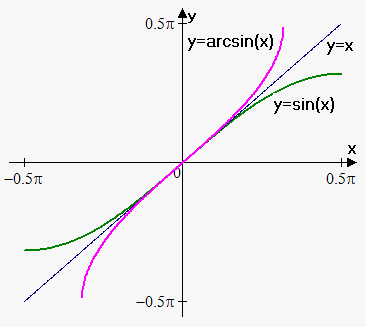and passes horizontal line test on this interval. Therefore, it has inverse.

We denote it by $$${\color{red}{{{y}={\operatorname{arcsin}{{\left({x}\right)}}}}}}$$$ (it is also often denoted by $$${y}={{\sin}}^{{-{1}}}{\left({x}\right)}$$$).

So, $$${y}={\operatorname{arcsin}{{\left({x}\right)}}}$$$ is equivalent to $$${\sin{{\left({y}\right)}}}={x},-\frac{\pi}{{2}}\le{y}\le\frac{\pi}{{2}}$$$.

Domain of the function $$${y}={\operatorname{arcsin}{{\left({x}\right)}}}$$$ is $$${\left[-{1},{1}\right]}$$$, range is $$${\left[-\frac{\pi}{{2}},\frac{\pi}{{2}}\right]}$$$.

As always, since $$${\sin{}}$$$ and $$${\operatorname{arcsin}{}}$$$ are inverse to each other, then their graph are symmetric about line $$${y}={x}$$$.

For function $$${y}={\cos{{\left({x}\right)}}}$$$ we take interval $$${\left[{0},\pi\right]}$$$. Function takes all values from range $$${\left[-{1},{1}\right]}$$$ 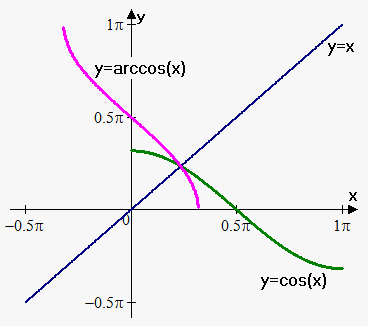and passes horizontal line test on this interval. Therefore, it has inverse.

We denote it as $$${\color{green}{{{y}={\operatorname{arccos}{{\left({x}\right)}}}}}}$$$ (it is also often denoted by $$${y}={{\cos}}^{{-{1}}}{\left({x}\right)}$$$).

So, $$${y}={\operatorname{arccos}{{\left({x}\right)}}}$$$ is equivalent to $$${\cos{{\left({y}\right)}}}={x},{0}\le{y}\le\pi$$$.

Domain of the function $$${y}={\operatorname{arccos}{{\left({x}\right)}}}$$$ is $$${\left[-{1},{1}\right]}$$$, range is $$${\left[{0},\pi\right]}$$$.

For function $$${y}={\tan{{\left({x}\right)}}}$$$ we take interval $$${\left(-\frac{\pi}{{2}},\frac{\pi}{{2}}\right)}$$$. Function takes all values 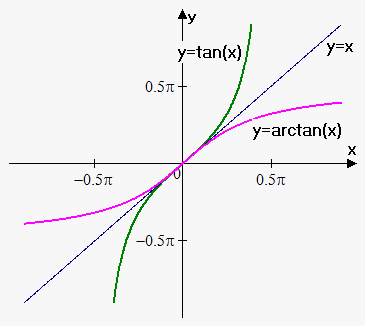and passes horizontal line test on this interval. Therefore, it has inverse.

We denote it as $$${\color{blue}{{{y}={\operatorname{arctan}{{\left({x}\right)}}}}}}$$$ (it is also often denoted by $$${y}={{\tan}}^{{-{1}}}{\left({x}\right)}$$$).

So, $$${y}={\operatorname{arctan}{{\left({x}\right)}}}$$$ is equivalent to $$${\tan{{\left({y}\right)}}}={x},-\frac{\pi}{{2}}<{y}<\frac{\pi}{{2}}$$$.

Domain of the function $$${y}={\operatorname{arctan}{{\left({x}\right)}}}$$$ is $$${\left(-\infty,\infty\right)}$$$, range is $$${\left(-\frac{\pi}{{2}},\frac{\pi}{{2}}\right)}$$$.

For function $$${y}={\cot{{\left({x}\right)}}}$$$ we take interval $$${\left({0},\pi\right)}$$$. Function takes all values and passes 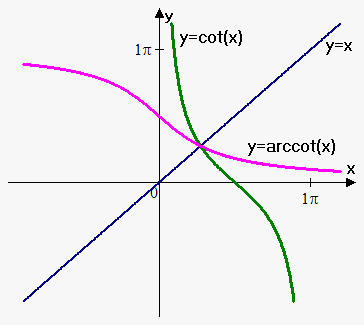horizontal line test on this interval. Therefore, it has inverse.

We denote it as $$${y}=\text{arccot}{\left({x}\right)}$$$ (it is also often denoted by $$${y}={{\cot}}^{{-{1}}}{\left({x}\right)}$$$).

So, $$${y}=\text{arccot}{\left({x}\right)}$$$ is equivalent to $$${\cot{{\left({y}\right)}}}={x},{0}<{y}<\pi$$$.

Domain of the function $$${y}=\text{arccot}{\left({x}\right)}$$$ is $$${\left(-\infty,\infty\right)}$$$, range is $$${\left({0},\pi\right)}$$$.