Volumes, Solids of Revolution and Method of Rings/Disks
In trying to find volume of the solid we use same approach as with area problem.
We divide solid into $$${n}$$$ pieces, approximate volume of each piece, take sum of volumes and then take limit as $$${n}\to\infty$$$.
We start from a simple fact: volume of cylinder, with area of base $$${A}$$$ and height $$${h}$$$ is $$${V}={A}{h}$$$.
In particular, circular cylinder, whose base is circle of radius $$${r}$$$ has volume $$${V}=\pi{{r}}^{{2}}{h}$$$. Rectangular box, whose base is rectangle with sides $$${a}$$$ and $$${b}$$$ has volume $$${V}={a}{b}{h}$$$.
Now, consider a general solid $$${S}$$$, that doesn't have a form of cylinder. We first "cut" it into $$${n}$$$ pieces (imagine a cucumber that is not a cylinder, that is cut into $$${n}$$$ pieces). Now, we approximate volume of each piece by volume of cylinder. We estimate the volume of $$${S}$$$ by adding the volumes of the cylinders. We obtain exact volume of $$${S}$$$ though a limiting process in which the number of pieces becomes very large.
We start by intersecting $$${S}$$$ with a plane and obtaining a plane region that is called a cross-section of $$${S}$$$. Let $$${A}{\left({x}\right)}$$$ be the area of the cross-section of $$${S}$$$ in a plane perpendicular to the x-axis and passing through the point $$${x}$$$, where $$${a}\le{x}\le{b}$$$. The cross-sectional area $$${A}{\left({x}\right)}$$$ will vary as $$${x}$$$ increases from a to b.
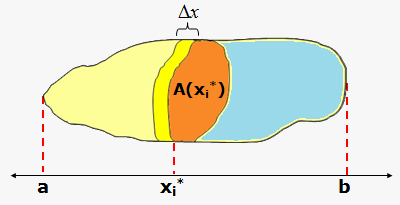
Let’s divide $$${S}$$$ into $$${n}$$$ "slabs" of equal width. (Think of slicing a loaf of bread.) If we choose sample points in $$${{x}_{{i}}^{{\star}}}$$$ in $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$, we can approximate the i-th slab by a cylinder with base area $$${A}{\left({{x}_{{i}}^{{\star}}}\right)}$$$ and "height" $$$\Delta{x}$$$.
The volume of this cylinder is $$${A}{\left({{x}_{{i}}^{{\star}}}\right)}\Delta{x}$$$, so an approximation to volume of the i-th slab is $$${V}{\left({S}_{{i}}\right)}\approx{A}{\left({{x}_{{i}}^{{\star}}}\right)}\Delta{x}$$$.
Adding the volumes of these slabs, we get an approximation to the total volume: $$${V}\approx{\sum_{{{i}={1}}}^{{n}}}{A}{\left({{x}_{{i}}^{{\star}}}\right)}\Delta{x}$$$.
This approximation appears to become better and better as $$${n}\to\infty$$$. (Think of the slices as becoming thinner and thinner.) Therefore, we define the volume as the limit of these sums as $$${n}\to\infty$$$: $$${V}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{A}{\left({{x}_{{i}}^{{\star}}}\right)}\Delta{x}$$$. But we recognize the limit of Riemann sums as a definite integral and so we have the following definition.
Definition of Volume. Let $$${S}$$$ be a solid that lies between $$${x}={a}$$$ and $$${x}={b}$$$. If the cross-sectional area of $$${S}$$$ through $$${x}$$$ and perpendicular to the x-axis, is $$${A}{\left({x}\right)}$$$, where $$${A}$$$ is a continuous function, then the volume of $$${S}$$$ is $$${V}={\int_{{a}}^{{b}}}{A}{\left({x}\right)}{d}{x}$$$.
It is important to remember that $$${A}{\left({x}\right)}$$$ is the area of a cross-section obtained by slicing through $$${x}$$$ perpendicular to the x-axis.
If we instead slice perpendicular to y-axis then $$${V}={\int_{{c}}^{{d}}}{A}{\left({y}\right)}{d}{y}$$$.
Example 1. Find volume of sphere of radius $$${r}$$$.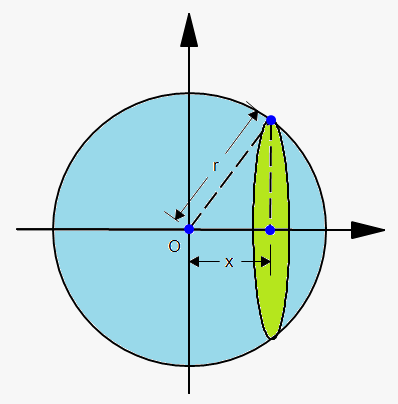
If we place the sphere so that its center is at the origin, then the cross-section is circle whose radius (from the Pythagorean
Theorem) is $$${y}=\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}$$$.
So, the cross-sectional area is $$${A}{\left({x}\right)}=\pi{{y}}^{{2}}=\pi{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}$$$.
Therefore, $$${V}={\int_{{-{r}}}^{{r}}}\pi{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}{d}{x}=\pi{\left({{r}}^{{2}}{x}-\frac{{1}}{{3}}{{x}}^{{3}}\right)}{{\mid}_{{-{r}}}^{{r}}}=$$$
$$$=\pi{\left({\left({{r}}^{{2}}\cdot{r}-\frac{{1}}{{3}}\cdot{{r}}^{{3}}\right)}-{\left({{r}}^{{2}}\cdot{\left(-{r}\right)}-\frac{{1}}{{3}}\cdot{{\left(-{r}\right)}}^{{3}}\right)}\right)}=$$$
$$$={2}\pi{\left({{r}}^{{3}}-\frac{{1}}{{3}}{{r}}^{{3}}\right)}=\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$.
Example 2. Find the volume of the solid whose base is a circle of radius $$${r}$$$ and whose cross-sections are equilateral triangles.
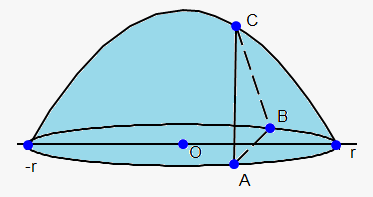
Let's take the circle $$${{x}}^{{2}}+{{y}}^{{2}}={r}$$$. Place its center at the origin.
Since B lies on the circle then $$${y}=\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}$$$ and so the base of triangle ABC is $$${\left|{A}{B}\right|}={2}\sqrt{{{1}-{{x}}^{{2}}}}$$$. Since triangle is equilateral then its area is $$${A}=\frac{{1}}{{2}}\cdot{\sin{{\left({{60}}^{{0}}\right)}}}\cdot{2}\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}\cdot{2}\sqrt{{{{r}}^{{2}}-{{x}}^{{2}}}}=$$$
$$$=\sqrt{{{3}}}{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}$$$.
So, cross-sectional area is $$${A}{\left({x}\right)}=\frac{{1}}{{2}}\cdot{2}\sqrt{{{1}-{{x}}^{{2}}}}\sqrt{{{3}}}{\left({1}-{{x}}^{{2}}\right)}=\sqrt{{{3}}}{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}$$$.
Therefore, $$${V}={\int_{{-{r}}}^{{r}}}\sqrt{{{3}}}{\left({{r}}^{{2}}-{{x}}^{{2}}\right)}{d}{x}=\sqrt{{{3}}}{\left({{r}}^{{2}}{x}-\frac{{1}}{{3}}{{x}}^{{3}}\right)}{{\mid}_{{-{r}}}^{{r}}}=\frac{{{4}{{r}}^{{3}}}}{{\sqrt{{{3}}}}}$$$.
Now, let's take a look at solids of revolution.
If we take some function $$${y}={f{{\left({x}\right)}}}$$$ and begin to revolve it around line, then we will obtain solid of revolution. In this case cross-sectional area is area of circle.
Note, that in example 1 we sphere can be treated as solid of revolution: revolving circle $$${{x}}^{{2}}+{{y}}^{{2}}={{r}}^{{2}}$$$ around x-axis.
In general, we calculate the volume of a solid of revolution by using the basic defining formula $$${V}={\int_{{a}}^{{b}}}{A}{\left({x}\right)}{d}{x}$$$ or $$${V}={\int_{{c}}^{{d}}}{A}{\left({y}\right)}{d}{y}$$$ and we find the cross-sectional area in one of the following ways: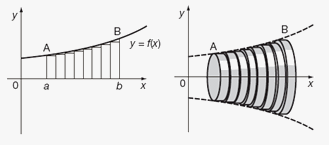
- If the cross-section is a disk then we use method of disks: we find the radius of the disk (in terms of $$${x}$$$ or $$${y}$$$) and use $$${A}=\pi{{\left({r}{a}{d}{i}{u}{s}\right)}}^{{2}}$$$.
- If the cross-section is a washer (also called ring) then we use method of rings: we find the inner radius $$${r}_{\text{in}}$$$ and outer radius $$${r}_{{{o}{u}{t}}}$$$ from a sketch and compute the area of the washer by subtracting the area of the inner disk from the area of the outer disk: $$${A}=\pi{{\left({r}_{{{o}{u}{t}}}\right)}}^{{2}}-\pi{{\left({r}_{{\text{in}}}\right)}}^{{2}}=\pi{\left({{\left({r}_{{{o}{u}{t}}}\right)}}^{{2}}-{{\left({r}_{{\text{in}}}\right)}}^{{2}}\right)}$$$.
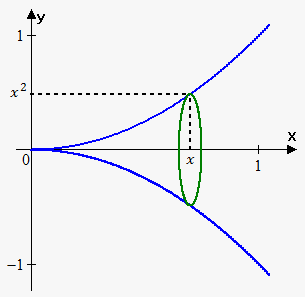 Example 3. Find the volume of the solid obtained by rotating about the x-axis the region under the curve $$${y}={{x}}^{{2}}$$$ from 0 to 1.
Example 3. Find the volume of the solid obtained by rotating about the x-axis the region under the curve $$${y}={{x}}^{{2}}$$$ from 0 to 1.
When we slice through the point $$${x}$$$, we get a disk with radius $$${{x}}^{{2}}.$$$
The area of this cross-section is $$${A}{\left({x}\right)}=\pi{{\left({{x}}^{{2}}\right)}}^{{2}}=\pi{{x}}^{{4}}$$$.
Therefore, $$${V}={\int_{{0}}^{{1}}}\pi{{x}}^{{4}}{d}{x}=\frac{\pi}{{5}}{{x}}^{{5}}{{\mid}_{{0}}^{{1}}}=\frac{\pi}{{5}}$$$.
Example 4. Find the volume of the solid obtained by rotating the region bounded by $$${y}={{x}}^{{2}}$$$, $$${y}={x}$$$ about the x-axis.
First we need to find points of intersection: $$${{x}}^{{2}}={x}$$$. From this we have that $$${x}={0}$$$ and $$${x}={1}$$$. So, points of intersection are $$${\left({0},{0}\right)}$$$ and $$${\left({1},{1}\right)}$$$.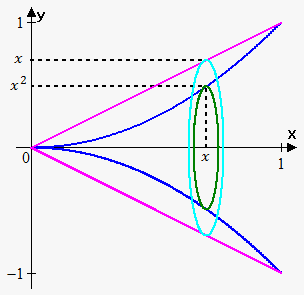
Since we rotate around x-axis, then we slice the solid perpendicular to the x-axis.
We have washer (ring) here, so if we slice at $$${x}$$$, then inner radius is $$${{x}}^{{2}}$$$ and outer radius is $$${x}$$$. So, the area of cross-section through $$${x}$$$ is $$${A}{\left({x}\right)}=\pi{\left({{\left({x}\right)}}^{{2}}-{{\left({{x}}^{{2}}\right)}}^{{2}}\right)}=\pi{\left({{x}}^{{2}}-{{x}}^{{4}}\right)}$$$.
Bounds of integration are 0 and 1 (we integrate with respect to $$${x}$$$).
Therefore, $$${V}={\int_{{0}}^{{1}}}\pi{\left({{x}}^{{2}}-{{x}}^{{4}}\right)}{d}{y}=\pi{\left(\frac{{1}}{{3}}{{x}}^{{3}}-\frac{{1}}{{5}}{{x}}^{{5}}\right)}{{\mid}_{{0}}^{{1}}}=\pi{\left(\frac{{1}}{{3}}-\frac{{1}}{{5}}\right)}=\frac{{2}}{{15}}\pi$$$.
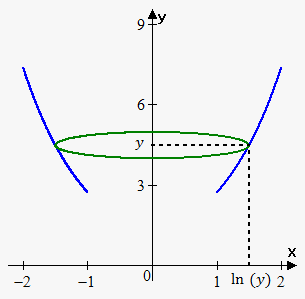 Example 5. Find the volume of the solid obtained by rotating about the y-axis the region under the curve $$${y}={{e}}^{{x}}$$$ from 1 to 2.
Example 5. Find the volume of the solid obtained by rotating about the y-axis the region under the curve $$${y}={{e}}^{{x}}$$$ from 1 to 2.
Since we rotate around y-axis, we need function in terms of $$${y}$$$ because cross-sectional area depends on $$${y}$$$: $$${x}={\ln{{\left({y}\right)}}}$$$.
When we slice through the point $$${y}$$$, we get a disk with radius $$${{\left({\ln{{\left({y}\right)}}}\right)}}^{{2}}$$$.
The area of this cross-section is $$${A}{\left({y}\right)}=\pi{{\left({\ln{{\left({y}\right)}}}\right)}}^{{2}}=\pi{{x}}^{{4}}$$$.
Bounds of integration are from $$${{e}}^{{1}}$$$ to $$${{e}}^{{2}}$$$.
Therefore, $$${V}={\int_{{e}}^{{{{e}}^{{2}}}}}\pi{{\left({\ln{{\left({y}\right)}}}\right)}}^{{2}}{d}{y}$$$.
This integral can be easily evaluated by applying integration by parts twice:
$$${V}=\pi{e}{\left({2}{e}-{1}\right)}$$$.
Example 6. Find the volume of the solid obtained by rotating the region bounded by $$${y}=\sqrt{{{x}}}$$$, $$${y}=\frac{{x}}{{2}}$$$ about the y-axis.
First we need to find points of intersection: $$$\sqrt{{{x}}}=\frac{{x}}{{2}}$$$ or $$${x}=\frac{{{{x}}^{{2}}}}{{4}}$$$. From this we have that $$${x}={0}$$$ and $$${x}={4}$$$. So, points of intersection are $$${\left({0},{0}\right)}$$$ and $$${\left({4},{2}\right)}$$$.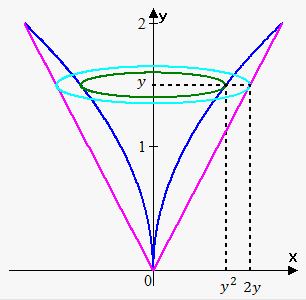
Since we rotate around y-axis, then we slice the solid perpendicular to the y-axis and rotate with respect to $$${y}$$$.
In this case cross-sectional area is function of $$${y}$$$ and we need to express functions in terms of $$${y}$$$: $$${x}={{y}}^{{2}}$$$ and $$${x}={2}{y}$$$.
We have washer (ring) here, so if we slice at height $$${y}$$$, then inner radius is $$${{y}}^{{2}}$$$ and outer radius is $$${2}{y}$$$. So, the area of cross-section through $$${y}$$$ is $$${A}{\left({y}\right)}=\pi{\left({{\left({2}{y}\right)}}^{{2}}-{{\left({{y}}^{{2}}\right)}}^{{2}}\right)}=\pi{\left({4}{{y}}^{{2}}-{{y}}^{{4}}\right)}$$$.
Bounds of integration are 0 and 2 (we integrate with respect to $$${y}$$$).
Therefore, $$${V}={\int_{{0}}^{{2}}}\pi{\left({4}{{y}}^{{2}}-{{y}}^{{4}}\right)}{d}{y}=\pi{\left(\frac{{4}}{{3}}{{y}}^{{3}}-\frac{{1}}{{5}}{{y}}^{{5}}\right)}{{\mid}_{{0}}^{{2}}}=\pi{\left(\frac{{32}}{{3}}-\frac{{32}}{{5}}\right)}=\frac{{64}}{{15}}\pi$$$.
Example 7. Find the volume of the solid obtained by rotating the region bounded by $$${y}={{x}}^{{2}}$$$, $$${y}={x}$$$ about the $$${y}={2}$$$.

As in example 4 points of intersection are $$${\left({0},{0}\right)}$$$ and $$${\left({1},{1}\right)}$$$, cross-section is a washer, but this time the inner radius is $$${2}-{x}$$$ and outer radius is $$${2}-{{x}}^{{2}}$$$.
The cross-sectional area is $$${A}{\left({x}\right)}=\pi{{\left({2}-{{x}}^{{2}}\right)}}^{{2}}-\pi{{\left({2}-{x}\right)}}^{{2}}=\pi{\left({{x}}^{{4}}-{5}{{x}}^{{2}}+{4}{x}\right)}$$$.
Therefore, $$${V}={\int_{{0}}^{{1}}}\pi{\left({{x}}^{{4}}-{5}{{x}}^{{2}}+{4}{x}\right)}{d}{x}=\pi{\left(\frac{{1}}{{5}}{{x}}^{{5}}-\frac{{5}}{{3}}{{x}}^{{3}}+{2}{{x}}^{{2}}\right)}{{\mid}_{{0}}^{{1}}}=$$$
$$$=\pi{\left(\frac{{1}}{{5}}-\frac{{5}}{{3}}+{2}\right)}=\frac{{{8}\pi}}{{15}}$$$.
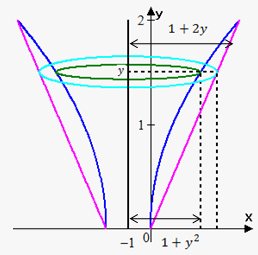 Example 8. Find the volume of the solid obtained by rotating the region bounded by the curves $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$ about the line $$${x}=-{1}$$$.
Example 8. Find the volume of the solid obtained by rotating the region bounded by the curves $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$ about the line $$${x}=-{1}$$$.
As in Example 6 points of intersection are $$${\left({0},{0}\right)}$$$ and $$${\left({4},{2}\right)}$$$.
Since we rotate about vertical line, then we need to express functions in terms of $$${y}$$$: $$${x}={{y}}^{{2}}$$$ and $$${x}={2}{y}$$$.
Now let's see what radii are. The distance from y-axis to inner function is $$${{y}}^{{2}}$$$, this means that distance from line $$${x}=-{1}$$$ to inner function is $$${1}+{{y}}^{{2}}$$$.
Similarly the distance from line $$${x}=-{1}$$$ to outer function (outer radius) is $$${1}+{2}{y}$$$.
Note, that it is very important to draw a sketch to correctly determine radii.
So, cross-sectional area is $$${A}{\left({y}\right)}=\pi{\left({{\left({1}+{2}{y}\right)}}^{{2}}-{{\left({1}+{{y}}^{{2}}\right)}}^{{2}}\right)}=\pi{\left({4}{y}+{2}{{y}}^{{2}}-{{y}}^{{4}}\right)}$$$.
Therefore, $$${V}={\int_{{0}}^{{2}}}\pi{\left({4}{y}+{2}{{y}}^{{2}}-{{y}}^{{4}}\right)}{d}{y}=\pi{\left({2}{{y}}^{{2}}+\frac{{2}}{{3}}{{y}}^{{3}}-\frac{{1}}{{5}}{{y}}^{{5}}\right)}{{\mid}_{{0}}^{{2}}}=\pi{\left({8}+\frac{{16}}{{3}}-\frac{{32}}{{5}}\right)}=\frac{{{104}\pi}}{{15}}$$$.
Example 9. Find volume of a cap of a sphere with radius $$${r}$$$ and height $$${h}$$$.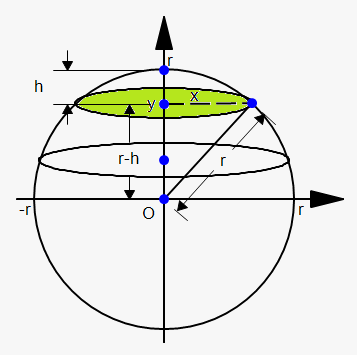
We need to find the top portion of the sphere of height $$${h}$$$, so, the cap starts at $$${y}={r}-{h}$$$ and ends at $$${y}={r}$$$.
If we slice perpendicular to y axis then each cross-section is circle with radius (according to Pythagorean theorem) $$${{x}}^{{2}}={{r}}^{{2}}-{{y}}^{{2}}$$$. Therefore, cross-sectional area is $$${A}{\left({y}\right)}=\pi{{x}}^{{2}}=\pi{\left({{r}}^{{2}}-{{y}}^{{2}}\right)}$$$.
Thus, $$${V}={\int_{{{r}-{h}}}^{{r}}}\pi{\left({{r}}^{{2}}-{{y}}^{{2}}\right)}{d}{y}=\pi{\left({{r}}^{{2}}{y}-\frac{{1}}{{3}}{{y}}^{{3}}\right)}{{\mid}_{{{r}-{h}}}^{{r}}}=$$$
$$$=\pi{\left({\left({{r}}^{{2}}\cdot{r}-\frac{{1}}{{3}}\cdot{{r}}^{{3}}\right)}-{\left({{r}}^{{2}}\cdot{\left({r}-{h}\right)}-\frac{{1}}{{3}}\cdot{{\left({r}-{h}\right)}}^{{3}}\right)}\right)}=$$$
$$$=\pi{{h}}^{{2}}{\left({r}-\frac{{1}}{{3}}{h}\right)}$$$. Note that when $$${h}={2}{r}$$$, we obtain volume of all sphere $$$\frac{{4}}{{3}}\pi{{r}}^{{3}}$$$.
