Triangle Calculator
Solve triangles step by step
The calculator will try to find all sides and angles of the triangle (right triangle, obtuse, acute, isosceles, equilateral), as well as its perimeter and area, with steps shown.
Our Triangle Calculator easily finds the sides and angles of a triangle with just a few inputs. If you want to deepen your understanding of triangles, our online tool is here.
How to Use the Triangle Calculator?
Input
Enter the known measurements of the triangle. This could include side lengths or angles.
Calculation
Once you've entered all the available information, click the "Calculate" button.
Result
The calculator will instantly provide results based on your input. This will include the missing side lengths, angles, perimeter, and area.
What Is a Triangle?
A triangle is a three-sided polygon. It is defined by its three straight sides and three internal angles. These angles always sum up to 180 degrees, regardless of the triangle's shape or size. Triangles can be categorized based on their sides and angles. Here are some standard classifications:
- Equilateral Triangle: All three sides are of equal length, and all three angles are 60 degrees.
- Isosceles Triangle: It has two sides of equal length, and the angles opposite those sides are also equal.
- Scalene Triangle: All sides have different lengths and all angles have different measures.
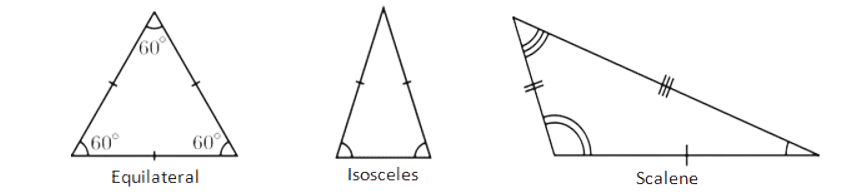
- Acute Triangle: All three angles are less than 90 degrees.
- Obtuse Triangle: One of the angles is greater than 90 degrees.
- Right-Angled Triangle: One of the angles is exactly 90 degrees, making it a right angle.

Triangles are fundamental shapes in geometry and have various properties and theorems associated with them.
What Are Some Key Facts, Theorems, and Laws Related to Triangles?
Facts about Triangles:
- Angle Sum: The sum of the interior angles of any triangle is always 180 degrees.
- Exterior Angle: An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Area Calculation: The area $$$A$$$ of a triangle with the side $$$b$$$ and the height $$$h$$$ dropped to this side can be found using the following formula:
$$A=\frac{1}{2}bh$$
Triangle Theorems:
Pythagorean Theorem (For Right Triangles): In a right triangle, the square of the length of the hypotenuse $$$c$$$ is equal to the sum of the squares of the lengths of the other two sides (called legs) $$$a$$$ and $$$b$$$. This can be represented as
$$c^2=a^2+b^2$$- Isosceles Triangle Theorem: In an isosceles triangle, the angles opposite the equal sides are also equal.
- Base Angles Theorem: The base angles are congruent in an isosceles triangle.
- Converse of the Base Angles Theorem: If two angles of a triangle are congruent, then the sides opposite those angles are also congruent, making it an isosceles triangle.
Triangle Laws
Law of Sines: For any triangle, the ratio of the length of a side to the sine of its opposite angle is constant. This can be written as
$$\frac{a}{\sin\left(A\right)}=\frac{b}{\sin\left(B\right)}=\frac{c}{\sin\left(C\right)}$$Law of Cosines: This rule relates the lengths of the sides of a triangle to the cosine of one of its angles. It can be used for any triangle, not just right triangles. Mathematically, it can be represented as
$$c^2=a^2+b^2-2ab\cos\left(C\right)$$$$b^2=a^2+c^2-2ac\cos\left(B\right)$$$$a^2=b^2+c^2-2bc\cos\left(A\right)$$Law of Tangents: For any triangle,
$$\frac{a-b}{a+b}=\frac{\tan\left(\frac{A-B}{2}\right)}{\tan\left(\frac{A+B}{2}\right)}$$
Understanding and applying these facts, theorems, and laws is critical to anyone who studies geometry. They provide insight into the properties of triangles and provide fundamental knowledge for more complex geometric concepts and real-world applications.
Why Choose Our Triangle Calculator?
Accuracy
Our calculator uses advanced algorithms to guarantee accuracy every time, giving you confidence in the results.
User-Friendly Interface
Built with user preferences in mind, our platform makes it easy to solve triangles, even for people new to geometry.
Versatility
Regardless of the type of triangle (scalene, isosceles, acute, or obtuse), our calculator will help you.
Fast Results
Our calculator provides answers almost instantly, making it much faster to solve multiple problems.
FAQ
How accurate are the results from the Triangle Calculator?
Our calculator uses advanced algorithms to ensure accurate and correct results.
Which types of triangles can this calculator handle?
Our Triangle Calculator is versatile and can handle various types of triangles, including scalene, isosceles, right, acute, and obtuse triangles.
What formulas does the Triangle Calculator use?
The calculator uses a variety of geometric formulas depending on the input, such as the Pythagorean theorem for right triangles, and the law of sines and cosines for others.
What is the Pythagorean Theorem?
The Pythagorean Theorem is a fundamental theorem in Euclidean geometry that describes the relationship between the three sides of a right triangle. It states that the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
