Work
Work is the total amount of effort required to perform a task.
In general, if an object moves along a straight line with position function $$${s}{\left({t}\right)}$$$, then the force $$${F}$$$ on the object (in the same direction) is defined by Newton’s Second Law of Motion as the product of its mass and its acceleration: $$${F}={m}\frac{{{{d}}^{{2}}{s}}}{{{d}{{t}}^{{2}}}}$$$.
In the SI metric system, the mass is measured in kilograms (kg), the displacement in meters (m), the time in seconds (s), and the force in newtons $$$\left({N}=\frac{{{k}{g{\cdot}}{m}}}{{{s}}^{{2}}}\right)$$$.
Thus, a force of 1 N acting on a mass of 1 kg produces an acceleration of 1 $$$\frac{{m}}{{{s}}^{{2}}}$$$.
In the U. S. System the fundamental unit is chosen to be the unit of force, which is the pound.
If force is constant then it is easy to calculate work: work is the product of the force and the distance that the object moves: $$${W}={F}{d}$$$.
If $$${F}$$$ is measured in newtons and $$${d}$$$ in meters, then the unit for $$${W}$$$ is a newton-meter, which is called a joule (J). If $$${F}$$$ is measured in pounds and $$${d}$$$ in feet, then the unit for $$${W}$$$ is a foot-pound (ft-lb), which is about 1.36 J.
For instance, suppose you lift a 1 kg bag off the floor to put it on a table that is 0.8 m high. The force you exert is equal and opposite to that exerted by gravity, so $$${F}={m}{g{=}}{1}\cdot{9.8}={9.8}\ {N}$$$ and $$${W}={F}{d}={9.8}\cdot{0.7}\approx{6.86}\ {J}$$$.
But if a 30-lb weight is lifted 7 ft off the ground, then the force is given as $$${F}={30}\ {l}{b}$$$, so the work done is $$${W}={F}{d}={30}\cdot{7}={120}\ {f{{t}}}-{l}{b}$$$.
Here we didn't multiply by $$${g{=}}{9.8}$$$ because we were given the weight (a force) and not the mass.
As can be seen there is no problem with calculating work, when force is constant, but what to do if work is variable?
Let's suppose that the object moves along the x-axis in the positive direction, from $$${x}={a}$$$ to $$${x}={b}$$$, and at each point $$${x}$$$ between $$${a}$$$ and $$${b}$$$ a force $$${f{{\left({x}\right)}}}$$$ acts on the object, where $$${f{}}$$$ is a continuous function.
We divide the interval $$${\left[{a},{b}\right]}$$$ into $$${n}$$$ subintervals with endpoints $$${x}_{{0}},{x}_{{1}},\ldots{x}_{{n}}$$$ and equal width $$$\Delta{x}=\frac{{{b}-{a}}}{{n}}$$$. We choose a sample point $$${{x}_{{i}}^{{\star}}}$$$ in the i-th subinterval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$. Then the force at that point is $$${f{{\left({{x}_{{i}}^{{\star}}}\right)}}}$$$. If $$${n}$$$ is large, then $$$\Delta{x}$$$ is small, and since $$${f{}}$$$ is continuous, the values of $$${f{}}$$$ don't change very much over the interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$. In other words, $$${f{}}$$$ is almost constant on the interval and so the work $$${W}_{{i}}$$$ that is done in moving the particle from $$${x}_{{{i}-{1}}}$$$ to $$${x}_{{i}}$$$ is $$${W}_{{i}}\approx{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}$$$. Thus, we can approximate the total work by $$${W}={\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{{\star}}}\right)}}}\Delta{x}$$$.
This approximation becomes better as we make $$${n}$$$ larger. Therefore, we define the work done in moving the object from $$${a}$$$ to $$${b}$$$ as the limit of this quantity as $$${n}\to\infty$$$: $$${W}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{f{{\left({{x}_{{i}}^{\star}}\right)}}}\Delta{x}$$$.
We recognize in this limit definite integral.
The work done in moving the object from $$${a}$$$ to $$${b}$$$ is $$${W}={\int_{{a}}^{{b}}}{f{{\left({x}\right)}}}{d}{x}$$$.
Example 1. When a particle is located at a distance $$${x}$$$ feet from the origin, a force of $$${{x}}^{{3}}+{1}$$$ pounds acts on it. How much work is done in moving it from $$${x}={2}$$$ to $$${x}={4}$$$?
$$${W}={\int_{{2}}^{{4}}}{\left({{x}}^{{3}}+{1}\right)}{d}{x}={\left(\frac{{1}}{{4}}{{x}}^{{4}}+{x}\right)}{{\mid}_{{2}}^{{4}}}={\left(\frac{{1}}{{4}}\cdot{{4}}^{{4}}+{4}\right)}-{\left(\frac{{1}}{{4}}\cdot{{2}}^{{4}}+{2}\right)}={62}$$$.
Thus, the work done is 62 ft-lb.
In the next example we use a law from physics: Hooke's Law states that the force required to maintain a spring stretched $$${x}$$$ units beyond its natural length is proportional to $$${x}$$$: $$${f{{\left({x}\right)}}}={k}{x}$$$ where $$${k}$$$ is a positive constant (called the spring constant).
Hooke's Law holds provided that $$${x}$$$ is not too large.
Example 2. A force of 60 N is required to hold a spring that has been stretched from its natural length of 5 cm to a length of 15 cm. How much work is done in stretching the spring from 15 cm to 20 cm?
According to Hooke's Law, the force required to hold the spring stretched $$${x}$$$ meters beyond its natural length is $$${f{{\left({x}\right)}}}={k}{x}$$$.
When the spring is stretched from 5 cm to 15 cm, the amount stretched is 10 cm=0.1m. This means that $$${f{{\left({0.1}\right)}}}={60}$$$, so $$${0.1}{k}={60}$$$ or $$${k}={600}$$$.
Therefore, $$${f{{\left({x}\right)}}}={600}{x}$$$.
Thus, the work done in stretching the spring from 15 cm to 20 cm is $$${W}={\int_{{0.1}}^{{{0.15}}}}{600}{x}{d}{x}={300}{{x}}^{{2}}{{\mid}_{{{0.1}}}^{{{0.15}}}}={300}{\left({{0.15}}^{{2}}-{{0.1}}^{{2}}\right)}={3.75}\ {J}$$$.
Example 3. Suppose that you have a rope that weighs $$${4}\frac{{{l}{b}{s}}}{{{f{{t}}}}}$$$. End of this rope of attached to the bucket. You drop bucket into the well and now it is full of water. Its weight is 30 lbs. Find the work done to lift a bucket if depth of well is 50 feet.
First we need to make convention about $$${x}$$$. Let $$${x}$$$ be the distance between ground and bucket. So, when $$${x}={0}$$$ bucket is in the bottom and when $$${x}={50}$$$ we are done.
At any point $$${x}$$$ we need to pull up $$${50}-{x}$$$ feets of rope plus bucket.
So, for any $$${x}$$$ force is $$${f{{\left({x}\right)}}}={4}{\left({50}-{x}\right)}+{30}={230}-{4}{x}$$$.
Now, the work done is $$${W}={\int_{{0}}^{{{50}}}}{\left({230}-{4}{x}\right)}{d}{x}={\left({230}{x}-{2}{{x}}^{{2}}\right)}{{\mid}_{{0}}^{{50}}}={130}\cdot{50}-{2}\cdot{{50}}^{{2}}={1500}\ {f{{t}}}-{l}{b}$$$.
Now let's see on a slightly harder example, where we need to understand how the work formula was derived.
Example 4. A tank has the shape of an inverted circular cone with height 10 m and base radius 5 m. It is filled with water to a height of 9 m. Find the work required to empty the tank by pumping all of the water to the top of the tank. (The density of water is 1000 $$$\frac{{{k}{g}}}{{{m}}^{{3}}}$$$).
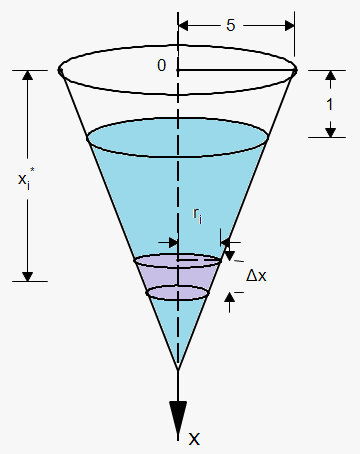
First of all we need to make convention about $$${x}$$$. Let $$${x}$$$ measure depths of tank. So, $$${x}={0}$$$ is top of the tank and $$${x}={10}$$$ is bottom of the tank. In this convention we see that water is in interval $$${\left[{1},{10}\right]}$$$.
Let's divide the interval $$${\left[{1},{10}\right]}$$$ into $$${n}$$$ subintervals with endpoints $$${x}_{{0}},{x}_{{1}},\ldots,{x}_{{n}}$$$ and choose $$${{x}_{{i}}^{{\star}}}$$$ in the i-th subinterval. This divides the water into $$${n}$$$ layers. The i-th layer (purple area) is approximated by a circular cylinder with radius $$${r}_{{i}}$$$ and height $$$\Delta{x}$$$. We can compute $$${r}_{{i}}$$$ from similar triangles: $$$\frac{{{r}_{{i}}}}{{{10}-{{x}_{{i}}^{{\star}}}}}=\frac{{5}}{{10}}$$$ or $$${r}_{{i}}=\frac{{1}}{{2}}{\left({10}-{{x}_{{i}}^{{\star}}}\right)}$$$.
Thus, an approximation to the volume of the i-th layer of water is $$${V}_{{i}}\approx\pi{{r}_{{i}}^{{2}}}\Delta{x}=\frac{\pi}{{4}}{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}$$$.
And so its mass is $$${m}_{{i}}=\text{density}\times\text{volume}\approx{1000}\frac{\pi}{{4}}{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}={250}\pi{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}$$$.
The force required to raise this layer must overcome the force of gravity, that is $$${F}_{{i}}={m}_{{i}}{g{}}$$$, where $$${g{=}}{9.8}\frac{{m}}{{{s}}^{{2}}}$$$, so $$${F}_{{i}}={m}_{{i}}{g{\approx}}{250}\pi{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}\cdot{9.8}={2450}\pi{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}$$$.
Each particle in the i-th layer must travel a distance of approximately $$${{x}_{{i}}^{{\star}}}$$$. The work done to raise this layer to the top is approximately the product of the force and the distance $$${{x}_{{i}}^{{\star}}}$$$: $$${W}_{{i}}\approx{F}_{{i}}{{x}_{{i}}^{{\star}}}={2450}\pi{{x}_{{i}}^{{\star}}}{{\left({10}-{{x}_{{i}}^{{\star}}}\right)}}^{{2}}\Delta{x}$$$.
To find the approximate total work done in emptying the entire tank, we add the contributions of each of the layers: $$${W}\approx{\sum_{{{i}={1}}}^{{n}}}{2450}\pi{{x}_{{i}}^{\star}}{{\left({10}-{{x}_{{i}}^{\star}}\right)}}^{{2}}\Delta{x}$$$.
To find actual work we need to take the limit as $$${n}\to\infty$$$: $$${W}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{2450}\pi{{x}_{{i}}^{\star}}{{\left({10}-{{x}_{{i}}^{\star}}\right)}}^{{2}}\Delta{x}$$$. We recognize in this limit definite integral, so
$$${W}={\int_{{1}}^{{{10}}}}{2450}\pi{x}{{\left({10}-{x}\right)}}^{{2}}{d}{x}={2450}\pi{\int_{{1}}^{{{10}}}}{\left({100}{x}-{20}{{x}}^{{2}}+{{x}}^{{3}}\right)}{d}{x}=$$$
$$$={2450}\pi{\left({50}{{x}}^{{2}}-\frac{{20}}{{3}}{{x}}^{{3}}+\frac{{1}}{{4}}{{x}}^{{4}}\right)}{{\mid}_{{1}}^{{{10}}}}={2450}\pi\cdot\frac{{3159}}{{4}}\approx{6.079}\times{{10}}^{{6}}\ {J}$$$.
