Volume of Solid of Revolution and Method of Cylinders
Sometimes it is very hard to use Method of Disks/Rings to obtain volume of solid of revolution.
But that's not a problem. We can use any shape for the cross section as long as it can be expanded or contracted to completely cover the solid.
In this note we introduce method of cylindrical shells.
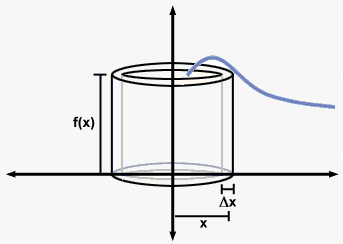 First suppose that we rotate about y-axis. Imagine a hollow cylinder whose wall has width $$$\Delta{x}$$$. In other words, imagine a rectangle of with $$$\Delta{x}$$$ rotated around y-axis. Radius of i-th cylinder is $$${r}{\left({{x}_{{i}}^{\star}}\right)}$$$ (it depends on $$${{x}_{{i}}^{\star}}$$$)where $$${{x}_{{i}}^{\star}}$$$ lies in interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$. On the figure radius is $$${r}{\left({{x}_{{i}}^{\star}}\right)}={{x}_{{i}}^{\star}}$$$.
First suppose that we rotate about y-axis. Imagine a hollow cylinder whose wall has width $$$\Delta{x}$$$. In other words, imagine a rectangle of with $$$\Delta{x}$$$ rotated around y-axis. Radius of i-th cylinder is $$${r}{\left({{x}_{{i}}^{\star}}\right)}$$$ (it depends on $$${{x}_{{i}}^{\star}}$$$)where $$${{x}_{{i}}^{\star}}$$$ lies in interval $$${\left[{x}_{{{i}-{1}}},{x}_{{i}}\right]}$$$. On the figure radius is $$${r}{\left({{x}_{{i}}^{\star}}\right)}={{x}_{{i}}^{\star}}$$$.
Imagine this shell to be cut and flattened. The resulting rectangular slab has length $$${2}\pi{r}{\left({{x}_{{i}}^{\star}}\right)}$$$ (length of circle with radius $$${r}{\left({{x}_{{i}}^{\star}}\right)}$$$), width $$$\Delta{x}$$$ and height $$${h}$$$ which depends on $$${{x}_{{i}}^{\star}}$$$ (on figure height is $$${f{{\left({{x}_{{i}}^{\star}}\right)}}}$$$).
So, the volume of the shell is $$${2}\pi{r}{\left({{x}_{{i}}^{\star}}\right)}{h}{\left({{x}_{{i}}^{\star}}\right)}\Delta{x}$$$.
If we do this for every subinterval and add the results, we get an approximation to the volume of the solid: $$${V}\approx{\sum_{{{i}={1}}}^{{n}}}{2}\pi{r}{\left({{x}_{{i}}^{\star}}\right)}{h}{\left({{x}_{{i}}^{\star}}\right)}\Delta{x}$$$.
This approximation improves as increases, so $$${V}=\lim_{{{n}\to\infty}}{\sum_{{{i}={1}}}^{{n}}}{2}\pi{r}{\left({{x}_{{i}}^{\star}}\right)}{h}{\left({{x}_{{i}}^{\star}}\right)}\Delta{x}$$$.
We recognize in this limit of Riemann sum definite integral, therefore $$${V}={\int_{{a}}^{{b}}}{2}\pi{r}{\left({x}\right)}{h}{\left({x}\right)}{d}{x}$$$.
Volume of solid rotated around y-axis is $$${V}={\int_{{a}}^{{b}}}{2}\pi{r}{\left({x}\right)}{h}{\left({x}\right)}{d}{x}$$$.
As can be seen the formula for area of the cross section in case of cylindrical shells is $$${A}={2}\pi{\left({r}{a}{d}{i}{u}{s}\right)}{\left({h}{e}{i}{g{{h}}}{t}\right)}$$$.
It is always a good practice to draw a sketch of problem in order to correctly determine radius and height.
In case we rotate around x-axis, radius and height will depend on $$${y}$$$.
Example 1. Find the volume of the solid obtained by rotating about the y-axis the region bounded by the curve $$${y}={4}{{\left({x}-{1}\right)}}^{{2}}{{\left({x}-{3}\right)}}^{{2}}$$$ and x-axis.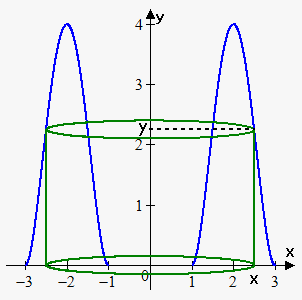
First of all note that we can't use method of disks here. Since we rotate about y-axis we need function in terms of $$${y}$$$, but it is very hard to express $$${x}$$$ in terms of $$${y}$$$.
Now we draw a sketch. In this case radius of cylinder is $$${x}$$$ and height is $$${y}{\left({x}\right)}={4}{{\left({x}-{1}\right)}}^{{2}}{{\left({x}-{3}\right)}}^{{2}}$$$.
Bounds of integration are 1 and 3.
Therefore, $$${V}={\int_{{1}}^{{3}}}{2}\pi{x}\cdot{4}{{\left({x}-{1}\right)}}^{{2}}{{\left({x}-{3}\right)}}^{{2}}{d}{x}=$$$
$$$={8}\pi{\int_{{1}}^{{3}}}{\left({{x}}^{{4}}-{8}{{x}}^{{3}}+{22}{{x}}^{{2}}-{24}{x}+{9}\right)}{d}{x}=$$$
$$$={8}\pi{\left(\frac{{1}}{{5}}{{x}}^{{5}}-{2}{{x}}^{{4}}+\frac{{22}}{{3}}{{x}}^{{3}}-{12}{{x}}^{{2}}+{9}{x}\right)}{{\mid}_{{1}}^{{3}}}=$$$
$$$={8}\pi{\left(\frac{{1}}{{5}}\cdot{{3}}^{{5}}-{2}\cdot{{3}}^{{4}}+\frac{{22}}{{3}}\cdot{{3}}^{{3}}-{12}\cdot{{3}}^{{2}}+{9}\cdot{3}\right)}-{8}\pi{\left(\frac{{1}}{{5}}\cdot{{1}}^{{5}}-{2}\cdot{{1}}^{{4}}+\frac{{22}}{{3}}\cdot{{1}}^{{3}}-{12}\cdot{{1}}^{{2}}+{9}\cdot{1}\right)}=\frac{{{128}\pi}}{{15}}$$$.
Next examples can be solved using method of disks, but we will solve them using cylindrical shells.
Example 2. Find the volume of the solid obtained by rotating about the y-axis the region bounded by the curves $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$.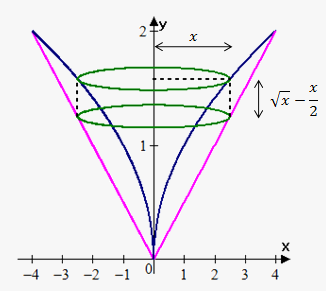
First we draw a sketch. In this case radius of cylinder is $$${x}$$$ and height is difference between function values at $$${x}$$$: $$${h}{\left({x}\right)}=\sqrt{{{x}}}-\frac{{x}}{{2}}$$$.
Bounds of integration are points of intersection of $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$, i.e. 0 and 4.
Therefore, $$${V}={\int_{{0}}^{{4}}}{2}\pi{x}\cdot{\left(\sqrt{{{x}}}-\frac{{x}}{{2}}\right)}{d}{x}={2}\pi{\int_{{0}}^{{4}}}{\left({{x}}^{{\frac{{3}}{{2}}}}-\frac{{1}}{{2}}{{x}}^{{2}}\right)}{d}{x}=$$$
$$$={2}\pi{\left(\frac{{2}}{{5}}{{x}}^{{\frac{{5}}{{2}}}}-\frac{{1}}{{6}}{{x}}^{{3}}\right)}{{\mid}_{{0}}^{{4}}}={2}\pi{\left(\frac{{2}}{{5}}\cdot{32}-\frac{{64}}{{6}}\right)}=\frac{{{64}\pi}}{{15}}$$$.
Example 3. Find the volume of the solid obtained by rotating about the line $$${x}=-{1}$$$ the region bounded by the curves $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$.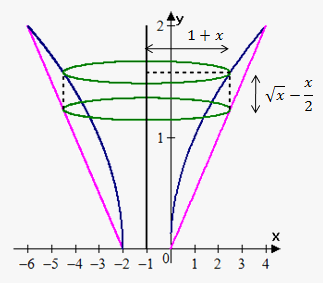
First we draw a sketch. In this case radius of cylinder is not $$${x}$$$, it is distance between line $$${x}=-{1}$$$ and edge of cylinder: $$${1}+{x}$$$. Height is $$${y}{\left({x}\right)}=\sqrt{{{x}}}-\frac{{x}}{{2}}$$$.
Bounds of integration are points of intersection of $$${y}=\sqrt{{{x}}}$$$ and $$${y}=\frac{{x}}{{2}}$$$, i.e. 0 and 4.
Therefore, $$${V}={\int_{{0}}^{{4}}}{2}\pi{\left({1}+{x}\right)}\cdot{\left(\sqrt{{{x}}}-\frac{{x}}{{2}}\right)}{d}{x}=$$$
$$$={2}\pi{\int_{{0}}^{{4}}}{\left({{x}}^{{\frac{{3}}{{2}}}}+{{x}}^{{\frac{{1}}{{2}}}}-\frac{{1}}{{2}}{{x}}^{{2}}-\frac{{1}}{{2}}{x}\right)}{d}{x}=$$$
$$$={2}\pi{\left(\frac{{2}}{{5}}{{x}}^{{\frac{{5}}{{2}}}}+\frac{{2}}{{3}}{{x}}^{{\frac{{3}}{{2}}}}-\frac{{1}}{{6}}{{x}}^{{3}}-\frac{{1}}{{4}}{{x}}^{{2}}\right)}{{\mid}_{{0}}^{{4}}}={2}\pi{\left(\frac{{64}}{{5}}+\frac{{16}}{{3}}-\frac{{64}}{{6}}-\frac{{16}}{{4}}\right)}=\frac{{{104}\pi}}{{15}}$$$.
Now let's see how to handle situations when we rotate about x-axis.
Example 4. Find the volume of the solid obtained by rotating about the x-axis the region bounded by the curve $$${y}={{x}}^{{2}}$$$ on interval $$${\left[{0},{1}\right]}$$$.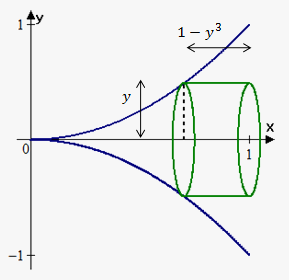
Since we rotate about x-axis, we need function in terms of $$${y}$$$: $$${x}=\pm\sqrt{{{y}}}$$$. Since we are in first quadrant (interval $$${\left[{0},{1}\right]}$$$) then we choose positive value $$${x}=\sqrt{{{y}}}$$$.
Now we draw a sketch. In this case radius of cylinder is $$${y}$$$ and height is distance from 1 to function, i.e. $$${h}{\left({y}\right)}={1}-\sqrt{{{y}}}$$$.
Bounds of integration are 0 and 1.
Therefore, $$${V}={\int_{{0}}^{{1}}}{2}\pi{y}\cdot{\left({1}-\sqrt{{{y}}}\right)}{d}{y}=$$$
$$$={2}\pi{\int_{{0}}^{{1}}}{\left({y}-{{y}}^{{\frac{{3}}{{2}}}}\right)}{d}{y}={2}\pi{\left(\frac{{1}}{{2}}{{y}}^{{2}}-\frac{{2}}{{5}}{{y}}^{{\frac{{5}}{{2}}}}\right)}{{\mid}_{{0}}^{{1}}}={2}\pi{\left(\frac{{1}}{{2}}-\frac{{2}}{{5}}\right)}=\frac{\pi}{{5}}$$$.
Example 5. Find the volume of the solid obtained by rotating about the x-axis the region bounded by the curves $$${y}={{x}}^{{2}}$$$ and $$${y}={x}$$$.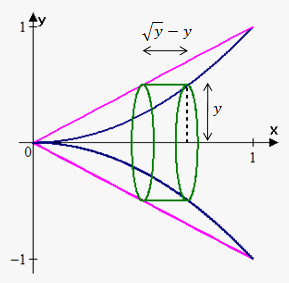
Since we rotate about x-axis, we need functions in terms of $$${y}$$$: $$${x}=\sqrt{{{y}}}$$$ and $$${x}={y}$$$.
Now we draw a sketch. In this case radius of cylinder is $$${y}$$$ and height is difference between outer and inner function at $$${y}$$$: $$${h}{\left({y}\right)}=\sqrt{{{y}}}-{y}$$$.
Bounds of integration are 0 and 1.
Therefore, $$${V}={\int_{{0}}^{{1}}}{2}\pi{y}{\left(\sqrt{{{y}}}-{y}\right)}{d}{y}=$$$
$$$={2}\pi{\int_{{0}}^{{1}}}{\left({{y}}^{{\frac{{3}}{{2}}}}-{{y}}^{{2}}\right)}{d}{y}={2}\pi{\left(\frac{{2}}{{5}}{{y}}^{{\frac{{5}}{{2}}}}-\frac{{1}}{{3}}{{y}}^{{3}}\right)}{{\mid}_{{0}}^{{1}}}={2}\pi{\left(\frac{{2}}{{5}}-\frac{{1}}{{3}}\right)}=\frac{{{2}\pi}}{{15}}$$$.
Example 6. Find the volume of the solid obtained by rotating about horizontal line $$${y}={2}$$$ the region bounded by the curves $$${y}={{x}}^{{2}}$$$ and $$${y}={x}$$$.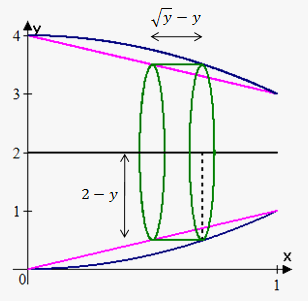
We again need functions in terms of $$${y}$$$: $$${x}=\sqrt{{{y}}}$$$ and $$${x}={y}$$$.
Bounds of integration are points of intersection of $$${x}=\sqrt{{{y}}}$$$ and $$${x}={y}$$$, i.e. 0 and 1.
Now we draw a sketch.
At $$${y}$$$ radius of cylinder is $$${2}-{y}$$$ and height is difference between values of outer and inner functions at $$${y}$$$: $$$\sqrt{{{y}}}-{y}$$$.
Therefore, $$${V}={\int_{{0}}^{{1}}}{2}\pi{\left({2}-{y}\right)}{\left(\sqrt{{{y}}}-{y}\right)}{d}{y}={2}\pi{\int_{{0}}^{{1}}}{\left({2}{{y}}^{{\frac{{1}}{{2}}}}+{{y}}^{{2}}-{2}{y}-{{y}}^{{\frac{{3}}{{2}}}}\right)}{d}{y}=$$$
$$$={2}\pi{\left(\frac{{4}}{{3}}{{y}}^{{\frac{{3}}{{2}}}}+\frac{{1}}{{3}}{{y}}^{{3}}-{{y}}^{{2}}-\frac{{2}}{{5}}{{y}}^{{\frac{{5}}{{2}}}}\right)}{{\mid}_{{0}}^{{1}}}={2}\pi{\left(\frac{{4}}{{3}}+\frac{{1}}{{3}}-{1}-\frac{{2}}{{5}}\right)}=\frac{{{8}\pi}}{{15}}$$$.
