Fermat's Theorem
Knowing derivative of function $$${f{{\left({x}\right)}}}$$$ allows us to make some conclusions about behavior of function $$${y}={f{{\left({x}\right)}}}$$$.
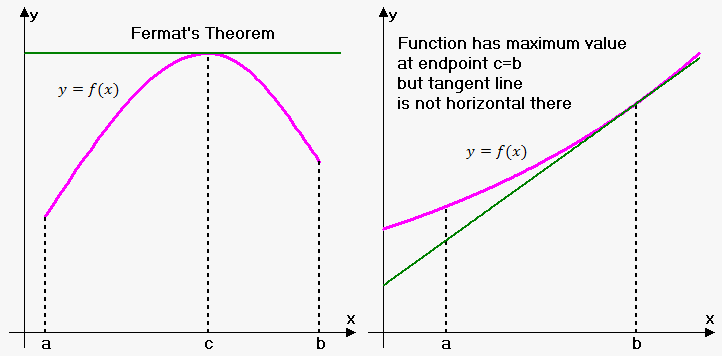
Fermat's Theorem. Suppose function $$$y={f{{\left({x}\right)}}}$$$ is defined on interval $$${\left[{a},{b}\right]}$$$ and at some point $$${c}\in{\left({a},{b}\right)}$$$ takes maximum (minimum) value. If exist finite derivative $$${f{'}}{\left({c}\right)}$$$ then $$${f{'}}{\left({c}\right)}={0}$$$.
Note, that converse of Fermat's Theorem is not true, that is, if $$${f{'}}{\left({c}\right)}={0}$$$ then $$${f{}}$$$ doesn't necessarily have maximum or minimum at $$${c}$$$.
For example, consider function $$${f{{\left({x}\right)}}}={{x}}^{{3}}$$$ then $$${f{'}}{\left({x}\right)}={3}{{x}}^{{2}}$$$ and $$${f{'}}{\left({x}\right)}={0}$$$ when $$${x}={0}$$$, but $$${x}={0}$$$ is neither maximum nor minimum. It is just a point where tangent line is horizontal and intersects graph.
Note that there may be maximum (or minimum) where $$${f{'}}{\left({c}\right)}$$$ does not exist. For instance, the function $$${f{{\left({x}\right)}}}={\left|{x}\right|}$$$ has its minimum value at 0, but the value cannot be found by setting $$${f{'}}{\left({x}\right)}={0}$$$ because $$${f{'}}{\left({0}\right)}$$$ does not exist.
Geometric interpretation of Fermat's theorem is fairly simple. Theorem states that if at point $$${c}$$$ there is maximum or minimum then tangent line at that point is horizontal, i.e. its slope equals 0.
Also, we require point $$${c}$$$ to be inner point of interval $$${\left[{a},{b}\right]}$$$. If point $$${c}$$$ is endpoint (either $$${a}$$$ or $$${b}$$$) then Fermat's theorem doesn't hold.