Even Odd Function
If $$${f{{\left({x}\right)}}}={f{{\left(-{x}\right)}}}$$$ for every $$${x}$$$ in the domain of $$${f{}}$$$ then f is an even function.
For example, $$${f{{\left({x}\right)}}}={{x}}^{{2}}$$$ is even because for every $$${x}$$$ $$${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{2}}={{x}}^{{2}}={f{{\left({x}\right)}}}$$$.
If $$${f{{\left(-{x}\right)}}}=-{f{{\left({x}\right)}}}$$$ for every $$${x}$$$ in the domain of $$${f{}}$$$ then $$${f{}}$$$ is an odd function.
For example, $$${f{{\left({x}\right)}}}={{x}}^{{5}}$$$ is odd because for every $$${x}$$$ $$${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{5}}=-{{x}}^{{5}}=-{f{{\left({x}\right)}}}$$$.
Consider graph of the two functions: $$${y}={{x}}^{{2}}$$$ and $$${y}=\frac{{1}}{{4}}{{x}}^{{3}}$$$.
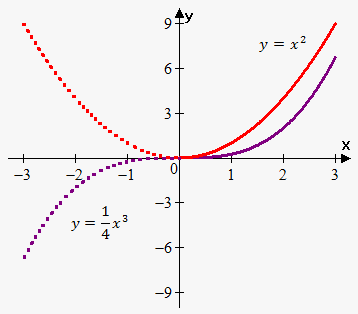
Since $$${y}={{x}}^{{2}}$$$ is even function then we draw it on interval $$${\left({0},\infty\right)}$$$ (red solid line) and then reflect it about y-axis (red dashed line)
Since $$${y}=\frac{{1}}{{4}}{{x}}^{{3}}$$$ is odd function then we draw it on interval $$${\left({0},\infty\right)}$$$ (purple solid line) and then reflect it about origin (purple dashed line). In other words we rotate graph $$${{180}}^{{0}}$$$ counterclockwise.
Example 1. Determine whether function $$${y}=\frac{{1}}{{{x}}^{{2}}}$$$ is even or odd.
Since $$${f{{\left(-{x}\right)}}}=\frac{{1}}{{{{\left(-{x}\right)}}^{{2}}}}=\frac{{1}}{{{x}}^{{2}}}={f{{\left({x}\right)}}}$$$ then function is even.
Example 2. Determine whether function $$${y}={{x}}^{{3}}-{x}$$$ is even or odd.
Since $$${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{3}}-{\left(-{x}\right)}={{x}}^{{3}}+{x}=-{\left({{x}}^{{3}}-{x}\right)}=-{f{{\left({x}\right)}}}$$$ then function is odd.
Example 3. Determine whether function $$${y}={{x}}^{{3}}+{{x}}^{{2}}$$$ is even or odd.
Since $$${f{{\left(-{x}\right)}}}={{\left(-{x}\right)}}^{{3}}+{{\left(-{x}\right)}}^{{2}}=-{{x}}^{{3}}+{{x}}^{{2}}$$$ then $$${f{{\left(-{x}\right)}}}\ne{f{{\left({x}\right)}}}$$$ and $$${f{{\left(-{x}\right)}}}\ne-{f{{\left({x}\right)}}}$$$. This means that function is neither even, nor odd.
