Inflection Points
Definition. Point $$$c$$$ is an inflection point of function $$$y={f{{\left({x}\right)}}}$$$ if function at this point changes direction of concavity (i.e. from concave upward becomes concave downward or from concave downward becomes concave upward).
It appears that $$${f{''}}{\left({x}\right)}$$$ plays same role in finding inflection points as played $$${f{'}}{\left({x}\right)}$$$ in finding extrema.
Fact. If point $$${c}$$$ is inflection point of the function $$${y}={f{{\left({x}\right)}}}$$$ then either $$${f{''}}{\left({c}\right)}={0}$$$ or $$${f{''}}{\left({c}\right)}$$$ doesn't exist.
Converse is not true. Consider function $$${f{{\left({x}\right)}}}={{x}}^{{4}}$$$. $$${f{''}}{\left({x}\right)}={12}{{x}}^{{2}}$$$, so $$${f{''}}{\left({0}\right)}={0}$$$, but $$${x}={0}$$$ is not 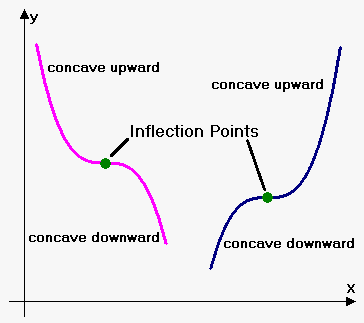 an inflection point.
an inflection point.
But we know that when $$${f{''}}{\left({x}\right)}>{0}$$$ function is concave upward, and when $$${f{''}}{\left({x}\right)}<{0}$$$ function is concave downward.
So, point will be point of inflection if second derivative changes sign at this point.
This rule is very similar to First Derivative Test for extrema.
Procedure for Finding Inflection Points:
- Find points where $$${f{''}}{\left({x}\right)}=0$$$ or $$${f{''}}{\left({x}\right)}$$$ doesn't exist.
- Test all points in the following way: if second derivative changes sign at point then it is point of inflection. Otherwise, it is not a point of inflection.
Now it is clear why $$${x}={0}$$$ is not point of inflection for $$${f{{\left({x}\right)}}}={{x}}^{{4}}$$$. That's because $$${f{''}}{\left({x}\right)}={12}{{x}}^{{2}}\ge{0}$$$ and second derivative doesn't change sign at $$${x}={0}$$$.
Example 1. Find points of inflection of $$${f{{\left({x}\right)}}}={{x}}^{{\frac{{1}}{{3}}}}$$$.
We have that $$${f{'}}{\left({x}\right)}=\frac{{1}}{{3}}{{x}}^{{-\frac{{2}}{{3}}}}$$$ and $$${f{''}}{\left({x}\right)}=-\frac{{2}}{{9}}{{x}}^{{-\frac{{5}}{{3}}}}$$$.
Second derivative is never zero, but it doesn't exist at $$${x}={0}$$$.
Since $$${f{''}}{\left({x}\right)}>{0}$$$ for $$${x}<{0}$$$ and $$${f{''}}{\left({x}\right)}<{0}$$$ for $$${x}>{0}$$$ then second derivative changes sign at $$${x}={0}$$$.
This means that $$${x}={0}$$$ is point of inflection.
Example 2. Find points of inflection of $$${f{{\left({x}\right)}}}={\sin{{\left({x}\right)}}}$$$.
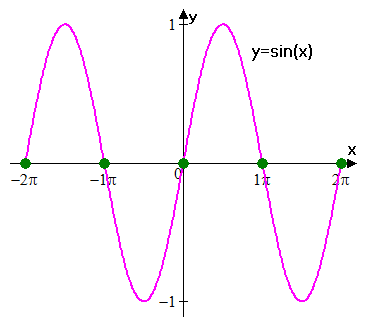 Since $$${f{'}}{\left({x}\right)}=-{\cos{{\left({x}\right)}}}$$$ and $$${f{''}}{\left({x}\right)}=-{\sin{{\left({x}\right)}}}$$$. then points of inflection are points where $$${\sin{{\left({x}\right)}}}={0}$$$ (clearly at these points second derivative changes sign).
Since $$${f{'}}{\left({x}\right)}=-{\cos{{\left({x}\right)}}}$$$ and $$${f{''}}{\left({x}\right)}=-{\sin{{\left({x}\right)}}}$$$. then points of inflection are points where $$${\sin{{\left({x}\right)}}}={0}$$$ (clearly at these points second derivative changes sign).
Thus, points of the form $$${x}=\pi{k},{k}\in\mathbb{Z}$$$ are points of inflection.
This means that $$${\sin{{\left({x}\right)}}}$$$ has infinite number of points of inflection.
Example 3. Find points of inflection of $$${f{{\left({x}\right)}}}={3}{{x}}^{{5}}-{5}{{x}}^{{4}}+{5}{x}-{7}$$$.
We have that $$${f{'}}{\left({x}\right)}={15}{{x}}^{{4}}-{20}{{x}}^{{3}}+{5}$$$ and $$${f{''}}{\left({x}\right)}={60}{{x}}^{{3}}-{60}{{x}}^{{2}}={60}{{x}}^{{2}}{\left({x}-{1}\right)}$$$.
Derivative is defined for all $$${x}$$$ so there are no such points where derivative doesn't exist.
So, inflection points are among roots of equation $$${f{''}}{\left({x}\right)}={0}$$$.
Equation $$${60}{{x}}^{{2}}{\left({x}-{1}\right)}={0}$$$ gives two roots: $$${x}={0}$$$ and $$${x}={1}$$$.
Now use method of intervals to where second derivative is positive and where negative.
Number line is divided by points $$${x}={0}$$$ and $$${x}={1}$$$ on 3 intervals: $$${\left(-\infty,{0}\right)}\cup{\left({0},{1}\right)}\cup{\left({1},\infty\right)}$$$.
First interval is $$${\left(-\infty,{0}\right)}$$$: here $$${{x}}^{{2}}>{0}$$$ and $$${x}-{1}<{0}$$$ so $$${f{''}}{\left({x}\right)}<{0}$$$.
Second interval is $$${\left({0},{1}\right)}$$$: here $$${{x}}^{{2}}>{0}$$$ and $$${x}-{1}<{0}$$$ so $$${f{''}}{\left({x}\right)}<{0}$$$.
First interval is $$${\left({1},\infty\right)}$$$: here $$${{x}}^{{2}}>{0}$$$ and $$${x}-{1}>{0}$$$ so $$${f{''}}{\left({x}\right)}>{0}$$$.
We see that derivative doesn't change sign at $$${x}={0}$$$ and changes sign from negative to positive at $$${x}={1}$$$.
This means that the only point of inflection is $$${x}={1}$$$.
As in case with extrema we can formulate criterion of finding inflection points using higher-order derivatives.
Fact. Suppose that for function $$${y}={f{{\left({x}\right)}}}$$$ there is point $$${c}$$$ such that $$${f{''}}{\left({c}\right)}={0}$$$. Also suppose $$${k}$$$ $$$\left({k}>{2}\right)$$$ is the smallest number such that $$${{f}}^{{{\left({k}\right)}}}{\left({c}\right)}\ne{0}$$$. If $$${k}$$$ is odd then $$${c}$$$ is point of inflection, if $$${k}$$$ is even then there is no point of inflection.
Let's solve Example 3 using above fact.
We have that $$${f{'''}}{\left({x}\right)}={180}{{x}}^{{2}}-{120}{x}$$$.
Since $$${f{'''}}{\left({1}\right)}={60}\ne{0}$$$ and 3 is odd number, then $$${x}={1}$$$ is point of inflection.
Since $$${f{'''}}{\left({0}\right)}={0}$$$, then third derivative is inconclusive for $$${x}={0}$$$.
Find fourth derivative $$${{f}}^{{{\left({4}\right)}}}{\left({x}\right)}={360}{x}-{120}$$$.
Since $$${{f}}^{{{\left({4}\right)}}}{\left({0}\right)}=-{120}\ne{0}$$$ and 4 is even number, then $$${x}={0}$$$ is not a point of inflection.
