Directional Derivative Calculator
Calculate directional derivatives step by step
The calculator will find the directional derivative (with steps shown) of the given function at the point in the direction of the given vector.
The Gradient and Directional Derivative: An Expert Guide
Introduction
In multivariable calculus, there are two important concepts that help us to understand functions in multiple dimensions: the gradient and the directional derivative. The gradient tells us about the rate at which a function changes, while the directional derivative allows us to explore how the function varies in a specific direction. In this article, we will understand these concepts and their significance and practical applications. Before this, let’s understand the gradient first.
Understanding of the Gradient
The gradient of a function, often represented as $$$\nabla f$$$ or $$$\operatorname{grad}(f)$$$, tells us about the direction and magnitude of the steepest slope of the function at a given point. It is a vector made up of partial derivatives, which show us how the function changes with each input variable.
Mathematically, the gradient is defined as:
$$\nabla f= \left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\ldots,\frac{\partial f}{\partial x_n}\right),$$where $$$f$$$ is a function with $$$n$$$ variables $$$\left(x_1,x_2,\ldots,x_n\right).$$$
The gradient of a function is calculated by finding partial derivatives of the function with respect to each variable involved. For example, the function $$$f(x,y)=3x^2+2y-5$$$ involves two variables $$$x$$$ and $$$y$$$. Let’s calculate the gradient of this function.
In the first step, calculate the partial derivatives of $$$f$$$ with respect to each variable:
$$\frac{\partial f}{\partial x}=6x$$$$\frac{\partial f}{\partial y}=2$$Now combine the partial derivatives into a vector to obtain the gradient:
$$\nabla f=\left(6x,2\right)$$The resulting gradient vector (∇f) represents the direction and magnitude of the steepest ascent of the function at any given point.
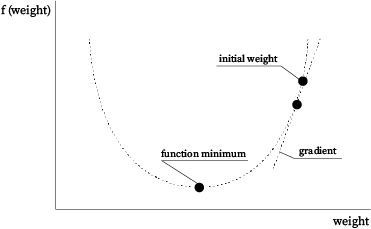
Geometric Interpretation of the Gradient
The gradient vector points to the direction of the steepness of a function or a curve at a specific point. In other words, it represents how steep the slope of the curve is. For example, the gradient of the following curve points toward the steepness. It will be in the form of a line pointing to the direction of the steepness of the curve.
Understanding the Directional Derivative
The directional derivative is the rate of change of a function along the unit vector at a specific point. It extends the idea of the derivative to understand the rate of change of a function in a specific direction. The directional derivative of a function $$$f$$$ in the direction of a unit vector $$$\mathbf{\vec{u}}$$$ is denoted as $$$D_{\mathbf{\vec{u}}}f$$$ or $$$\nabla f \cdot \mathbf{\vec{u}}$$$. We can compute it using the dot product of the gradient and the unit vector.
$$D_{\mathbf{\vec{u}}}f=\nabla f \cdot \mathbf{\vec{u}}=\frac{\partial f}{\partial x_1}\cdot u_1+\frac{\partial f}{\partial x_2}\cdot u_2+\ldots +\frac{\partial f}{\partial x_n}\cdot u_n,$$where $$$\mathbf{\vec{u}}=\left(u_1,u_2,\ldots,u_n\right)$$$ is a unit vector that represents the desired direction.
For example, let's calculate the directional derivative of the function $$$f(x,y)=3x^2+2y-5$$$ in the direction of $$$\mathbf{\vec{v}}=(1,1)$$$.
Start with the given function $$$f(x,y)$$$ and the specified direction vector $$$\mathbf{\vec{v}}=(1,1)$$$.
Calculate the gradient of $$$f$$$ using the steps mentioned earlier: $$$\nabla f=(6x,2)$$$.
Find the unit vector $$$\mathbf{\vec{u}}$$$ in the direction of the vector $$$\mathbf{\vec{v}}$$$: $$$\mathbf{\vec{u}}=\frac{\mathbf{\vec{v}}}{\left|\mathbf{\vec{v}}\right|}=\frac{(1,1)}{\sqrt{1^2+1^2}}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$$.
Compute the dot product of the gradient vector and the unit direction vector: $$$D_{\mathbf{\vec{u}}}f=\nabla f\cdot \mathbf{\vec{u}}=(6x,2)\cdot\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)=\frac{6x+2}{\sqrt{2}}$$$.
The resulting value $$$\frac{6x+2}{\sqrt{2}}$$$ represents the directional derivative of the function in the specified direction.
Interpreting the Directional Derivative
The directional derivative tells us the rate of change of a function in a specific direction. It helps us understand how the function behaves along a particular path and responds to changes in specific variables.
Relationship Between the Gradient and the Directional Derivative
Since both the directional derivative and the gradient are related to derivatives. Therefore, both have many similarities and dissimilarities. Let’s discuss their relationship in the following table.
| Gradient | Directional Derivative |
| The gradient is the measure of steepness of the slope of a function or a curve. | The directional derivative is the rate of change of a function in a specific direction. |
| The gradient is always perpendicular to the level curves or surfaces of the function. | The directional derivative is highest when the direction of the unit vector $$$\mathbf{\vec{u}}$$$ aligns with the gradient vector. |
| The magnitude of the gradient indicates the rate at which the function changes. | The maximum magnitude of the directional derivative is the magnitude of the gradient. |
Applications of the Gradient and Directional Derivative
The gradient and directional derivatives have various practical applications in fields like physics, engineering, and optimization algorithms. Here are a few examples:
Optimization
The gradient helps guide optimization algorithms, such as gradient descent, to efficiently find the minimum or maximum of a function. It shows the direction of the steepest descent or ascent.
Level Curves and Surfaces
The gradient is perpendicular to the level curves or surfaces of a function. This property is useful for creating contour plots and visualizing functions in higher dimensions.
Fluid Flow Analysis
The directional derivative is used in analyzing fluid flow, helping us understand how a fluid moves in a particular direction.
Conclusion
The gradient and directional derivatives are fundamental concepts in multivariable calculus that offer valuable insights into how functions change and behave in specific directions. Their applications span across various fields, making them indispensable tools for understanding and optimizing complex systems. By grasping these concepts, we unlock a deeper understanding of the mathematics that govern our multidimensional world.
