Instantaneous Rate of Change Calculator

The Instantaneous Rate of Change Calculator is a tool for understanding how a function changes at a specific point. Understanding the rate of change of a function, especially at a particular point, can be challenging. However, our calculator simplifies this process, making it more understandable for users.

How to Use the Instantaneous Rate of Change Calculator?

• Input

  Enter the function you want to analyze. Ensure that the function is correctly formatted, following standard mathematical notation. Then, provide the value of the зoint at which you want to determine the function's instantaneous rate of change. This represents the exact place on the graph of the function where you are interested in the rate of change.

• Calculation

  Click the "Calculate" button to start the calculation process.

• Result

  The calculator will display the result – the instantaneous rate of change of the given function at the specified point.

What is the Instantaneous Rate of Change?

The concept of instantaneous rate of change is fundamental and closely related to the field of calculus. Instantaneous rate of change shows how a function behaves at a specific point by measuring the exact rate at which its output changes relative to its input.

The formula for calculating the instantaneous rate of change at a specific point can be written as follows:

$$\lim_{h\to0}\frac{f(a+h)-f(a)}{h},$$

where:

• $$$a$$$ is the point of interest.
• $$$f(a)$$$ is the value of the function at the point $$$x=a$$$.
• $$$h$$$ is a slight change in the input.

The formula represents the average rate of the function over the interval $$$[a,a+h]$$$. But as $$$h\to0$$$, the interval becomes very small. In other words, for an infinitesimal change in the input data, we get an instantaneous rate of change.

For example, consider the function $$$f(x)=x^2$$$. We want to find the instantaneous rate of change at $$$x=3$$$.

$$\lim_{h\to0}\frac{(3+h)^2-3^2}{h}=\lim_{h\to0}\frac{9+6h+h^2-3^2}{h}=\lim_{h\to0}\frac{6h+h^2}{h}=\lim_{h\to0}\left(6+h\right)=6+0=6$$

So, at $$$x=3$$$, the rate of change of the function $$$f(x)=x^2$$$ is $$$6$$$.

This example demonstrates how the concept of instantaneous rate of change allows us to pinpoint how functions or real systems evolve at specific points, providing valuable information about their behavior. Calculus provides the mathematical tools to perform such precise calculations, allowing us to solve various scientific and engineering problems.

As can be seen, instantaneous rate of change of a function $$$f(x)$$$ at the point $$$x=a$$$ is the derivative of the function evaluated at $$$x=a$$$.

For the above example, $$$f^{\prime}(x)=2x$$$ and $$$f^{\prime}(3)=2\cdot3=6$$$.

Instantaneous Rate of Change on a Graph

Since the instantaneous rate of change of a function $$$f(x)$$$ at the point $$$x=a$$$ equals $$$f^{\prime}(a)$$$, it also equals the slope of the function at that point. This gives us an idea of the behavior of the function in the neighborhood of the point.

For example, consider the graph of the function $$$f(x)=x^2$$$ and its derivative $$$f^{\prime}(x)=2x$$$.

The slope of the curve at any given point represents the instantaneous rate of change of the function at that point. Put simply, it tells us how steep or shallow the function is at that point. The slope is determined by finding the tangent line, which is a straight line that touches the curve at just one point without crossing it.

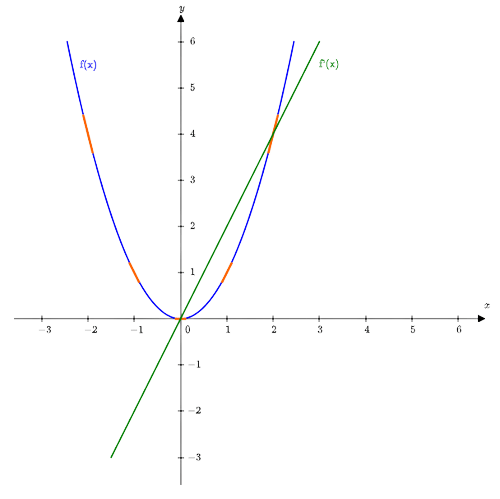
On this graph:

• At $$$x=-2$$$, $$$f^{\prime}(-2)=-4$$$. The slope of the tangent line is $$$-4$$$, the instantaneous rate of change is negative and very steep.
• At $$$x=-1$$$, $$$f^{\prime}(-1)=-2$$$. The slope of the tangent line is $$$-2$$$, the instantaneous rate of change is negative and relatively steep.
• At $$$x=0$$$, $$$f^{\prime}(0)=0$$$. The slope of the tangent line is $$$0$$$, the instantaneous rate of change is zero.
• At $$$x=1$$$, $$$f^{\prime}(1)=2$$$. The slope of the tangent line is $$$2$$$, the instantaneous rate of change is positive and relatively steep.
• At $$$x=2$$$, $$$f^{\prime}(2)=4$$$. The slope of the tangent line is $$$4$$$, the instantaneous rate of change is positive and very steep.

This graph visually represents the instantaneous rate of change, showing how it changes at different points.

Why Choose Our Instantaneous Rate of Change Calculator?

• Accuracy

  Our calculator uses rigorous mathematical principles to ensure accurate results.

• User-Friendly Interface

  Inputting the function and the point of interest is straightforward.

• Efficiency

  With fast calculations, our calculator is ideal for people who want to save time.

FAQ